X X 1 X 2
khabri
Sep 10, 2025 · 6 min read
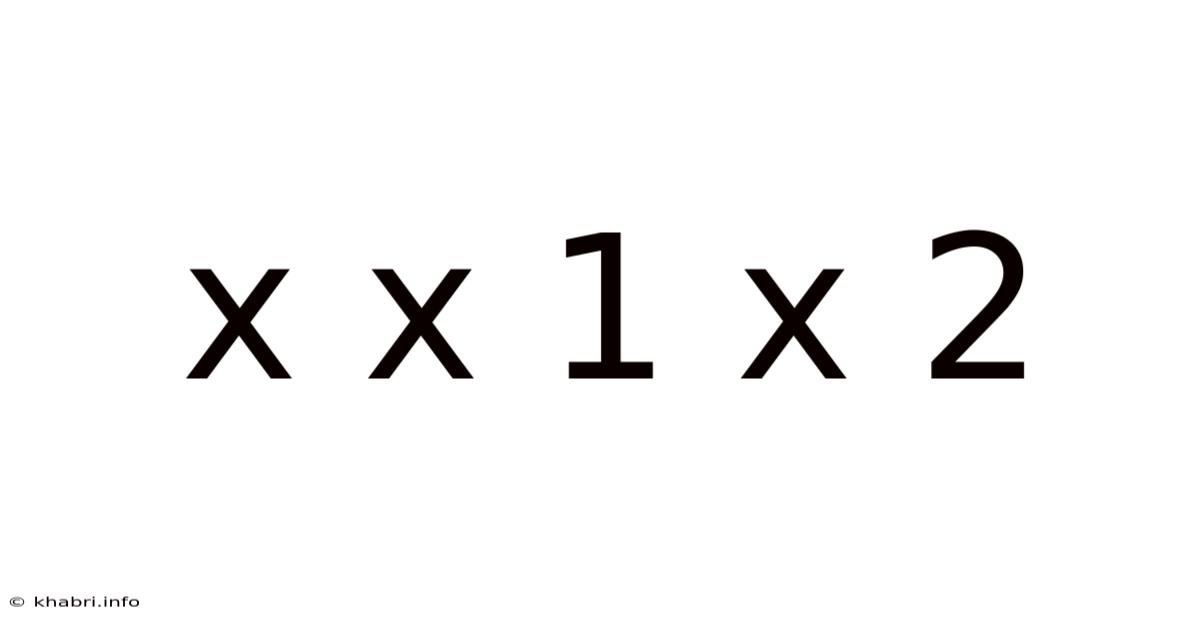
Table of Contents
Decoding the Mystery: A Deep Dive into x x 1 x 2
This article explores the intriguing mathematical concept represented by "x x 1 x 2," delving into its various interpretations and applications across different mathematical fields. We'll unpack its meaning in algebra, calculus, probability, and even touch upon its relevance in computer science and data analysis. Understanding this seemingly simple expression unlocks a door to a wealth of mathematical knowledge, proving that even the most basic structures can hold profound significance.
Introduction: Understanding the Ambiguity and Potential Meanings
At first glance, "x x 1 x 2" appears deceptively simple. However, its interpretation hinges heavily on context. The expression lacks explicit operators, leaving room for multiple valid interpretations depending on the mathematical framework being used. This ambiguity, far from being a weakness, actually highlights the richness and flexibility of mathematical notation. We will examine several possible interpretations, starting with the most straightforward and progressing to more complex scenarios.
Interpretation 1: Simple Multiplication
The most basic interpretation treats "x x 1 x 2" as a straightforward multiplication problem. In this case, the expression simplifies to:
x * x * 1 * 2 = 2x²
This is a fundamental algebraic expression, representing a parabola when graphed. Its properties are well-understood: it’s a quadratic function, meaning its highest power of x is 2. The coefficient 2 indicates the parabola's vertical scaling; it stretches the graph vertically compared to the simpler parabola y = x². The graph's vertex is at the origin (0,0), and it opens upwards.
This simple interpretation, while seemingly trivial, serves as a foundational building block for more complex calculations and concepts. It's crucial in understanding polynomials, solving quadratic equations, and working with various mathematical models.
Interpretation 2: Implicit Operations and Order of Operations (PEMDAS/BODMAS)
Let's consider a slightly more nuanced perspective. If we introduce implicit multiplication, where the juxtaposition of variables implies multiplication, we might interpret "x x 1 x 2" as:
x * (x * 1) * 2 = 2x²
This interpretation still leads to the same result, 2x², reaffirming the power of the order of operations (PEMDAS/BODMAS). The order in which we perform the multiplications doesn't change the final outcome in this particular case. However, this emphasis on order of operations becomes crucial when dealing with more complex expressions involving addition, subtraction, division, exponents, and parentheses. Mastering the order of operations is fundamental to accurately solving any mathematical problem.
Interpretation 3: Vectors and Matrices (Linear Algebra)
Moving beyond simple algebra, we can explore the possibility of "x x 1 x 2" representing vectors or matrices. If 'x' itself represents a vector or matrix, the interpretation becomes significantly more complex and requires specifying the type of multiplication used (scalar multiplication, dot product, cross product, or matrix multiplication).
For instance, if 'x' is a 2x1 column vector:
x = [[x₁], [x₂]]
And "1" and "2" are scalar multipliers, then:
x x 1 x 2 could represent 2 * [[x₁], [x₂]] = [[2x₁], [2x₂]] (scalar multiplication)
However, without a clear definition of 'x' and the type of multiplication intended, this interpretation remains highly speculative. This example highlights the importance of precise notation in advanced mathematical fields.
Interpretation 4: Functions and Mapping (Calculus)
Consider the case where 'x' is not a single value, but a variable representing a function or an independent variable in a function. For example, let's say we have a function f(x) = x.
Then "x x 1 x 2" could represent:
-
A composition of functions: This interpretation is highly context-dependent. There is no standard way to interpret this as a composition without further information. Are we dealing with a composition of multiple functions, a mapping between sets, or something else?
-
A transformation of a function: We might interpret the "x x 1 x 2" as part of a transformation on the function f(x). Again, the precise meaning depends on the mathematical context. For example, the "x x 1 x 2" might be part of a linear transformation applied to a vector space of functions.
To clarify such an interpretation, additional context and explicit functional notations are crucial.
Interpretation 5: Probability and Combinatorics
While less obvious, "x x 1 x 2" might find application in probability or combinatorics, particularly if 'x' represents a number of choices or events. For instance, if 'x' represents the number of ways to choose an item from a set, and we have two additional choices (represented by 1 and 2), the expression might be part of a larger combinatorial calculation to determine the total number of possibilities. However, this application remains highly dependent on the specifics of the problem.
Interpretation 6: Computer Science and Data Analysis
In programming or data analysis, "x x 1 x 2" could represent a sequence of operations performed on a data structure or variable 'x'. The specific meaning depends heavily on the programming language and the context of the code. For example:
- It might represent a sequence of array manipulations.
- It might indicate repeated operations within a loop.
- It might be part of a more complex algorithm.
Without the context of the surrounding code, it's impossible to definitively interpret this expression in a computational setting.
Frequently Asked Questions (FAQ)
Q: What is the most common interpretation of "x x 1 x 2"?
A: The most straightforward interpretation is simple multiplication, resulting in 2x².
Q: Does the order of multiplication matter in this expression?
A: In this specific case, due to the commutative property of multiplication, the order does not affect the final result. However, this is not true in general for all mathematical expressions.
Q: How can I understand the different interpretations better?
A: By studying different branches of mathematics like algebra, calculus, linear algebra, probability, and computer science, you can see how the same basic expression can have significantly different meanings based on context.
Q: Are there any limitations to these interpretations?
A: Yes, each interpretation has limitations based on the context. The lack of explicit operators limits precise interpretation without additional information.
Q: Can "x x 1 x 2" represent something other than numerical values?
A: Yes, 'x' could represent vectors, matrices, functions, or other mathematical objects, drastically altering the interpretation.
Conclusion: The Power of Context in Mathematics
The expression "x x 1 x 2" serves as a powerful illustration of how context is paramount in mathematics. While a simplistic view suggests a straightforward multiplication leading to 2x², the reality is far more nuanced. Its meaning changes drastically depending on the mathematical framework being employed – whether it's elementary algebra, linear algebra, calculus, probability, or computer science. Understanding this ambiguity encourages critical thinking and a deeper appreciation of the underlying structure and flexibility of mathematical notation. It underscores the need for precise and unambiguous language when communicating mathematical concepts, ensuring clear and consistent interpretations. The seemingly simple expression "x x 1 x 2" opens a door to a broader understanding of mathematical principles and their diverse applications across various fields.
Latest Posts
Latest Posts
-
Label The Referred Pain Pathway
Sep 10, 2025
-
3z 5 2z 25 5z
Sep 10, 2025
-
Franchising Is A Type Of
Sep 10, 2025
-
Body Dysmorphia Is A
Sep 10, 2025
-
Difference Between Ribose And Deoxyribose
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X X 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.