3z 5 2z 25 5z
khabri
Sep 10, 2025 · 5 min read
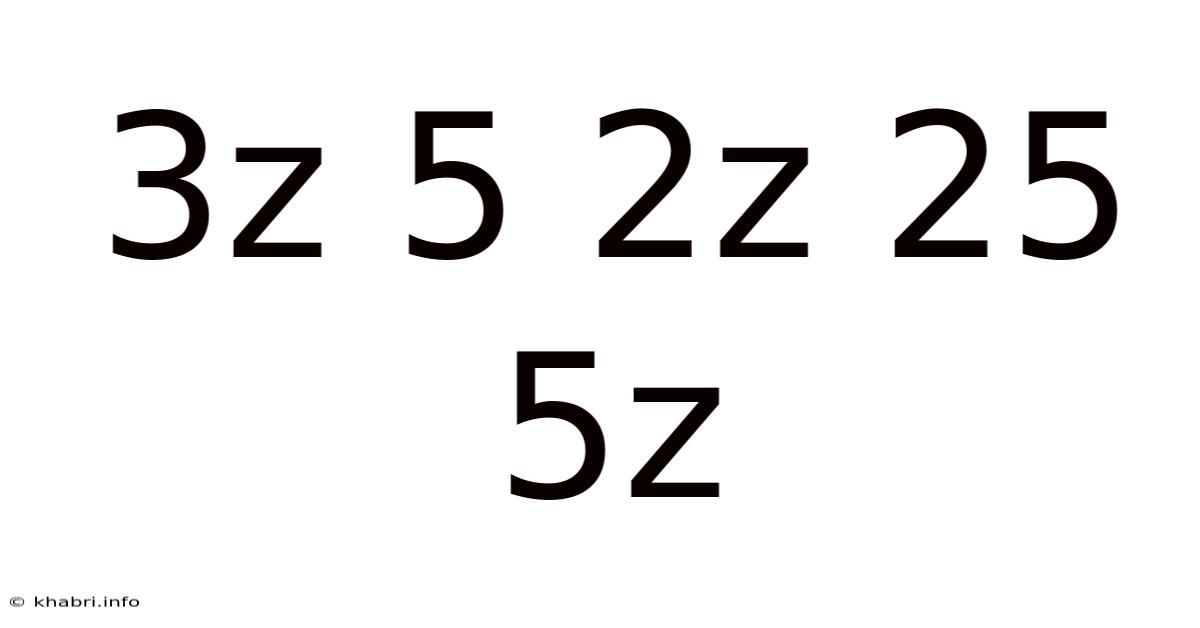
Table of Contents
Decoding the Sequence: Exploring the Mathematical Puzzle of 3z, 5, 2z, 25, 5z
This article delves into the intriguing mathematical sequence: 3z, 5, 2z, 25, 5z. We will explore various approaches to understanding the pattern, considering potential mathematical operations and relationships between the terms. This seemingly simple sequence presents a fascinating challenge, requiring us to think critically and creatively about the underlying logic. Understanding this sequence involves a blend of pattern recognition, algebraic manipulation, and a touch of deductive reasoning. Let's unravel the mystery together!
Understanding the Components: Variables and Constants
Before we dive into solving the puzzle, let's clarify the components. The sequence contains both variables and constants. The variable 'z' represents an unknown value, while the numbers 5 and 25 are constants. The challenge lies in determining the value of 'z' and the relationship between the terms. We need to find a consistent rule or pattern that connects all five elements within this sequence.
Methodical Approaches to Solving the Sequence
Several approaches can be used to tackle this sequence. We'll explore a few of the most common and effective methods:
1. Looking for Arithmetic Progressions or Geometric Progressions:
Initially, we might look for a straightforward arithmetic progression (a constant difference between consecutive terms) or a geometric progression (a constant ratio between consecutive terms). However, this sequence doesn't immediately conform to either of these standard patterns. The presence of the variable 'z' adds a layer of complexity.
2. Exploring Algebraic Relationships:
Since we have a variable, an algebraic approach is likely necessary. Let's explore potential relationships between the terms, considering the following possibilities:
-
Linear Relationships: Could there be a linear equation that connects consecutive terms or relates the terms to 'z'? For instance, we might hypothesize a relationship like:
Term_n = az + b, where 'a' and 'b' are constants, and 'n' represents the term's position in the sequence. This would provide a framework for determining the value of 'z' and the overall pattern. -
Quadratic Relationships: A more complex relationship might involve a quadratic equation. This approach would require more sophisticated algebraic manipulation but remains a viable option if a linear relationship fails to provide a satisfactory solution. We would look for a pattern involving z² in the terms.
-
Combinations of Operations: It's possible the sequence involves a combination of arithmetic and algebraic operations. Perhaps a specific mathematical operation is applied to one term to obtain the subsequent term, or the relationship might include some form of modular arithmetic.
3. Trial and Error and Systematic Guessing:
In the absence of an immediately apparent pattern, a more systematic trial-and-error approach can be surprisingly effective. By assigning different values to 'z', we can observe the resulting sequence and see if a consistent pattern emerges. It's important to be methodical in this process, documenting the results of each trial to avoid redundancy and identify any trends. This might involve writing a simple program to test various 'z' values and analyze the output sequence.
A Deeper Dive into Potential Solutions
Let's examine several possible scenarios and how they might resolve this sequence.
Scenario 1: Focusing on the Constant Terms
Notice that 5 and 25 are present in the sequence. 25 is a multiple of 5 (5 x 5 = 25). This might suggest a relationship between the constant terms and the variable 'z'. We need to look for connections between this relationship and the terms involving 'z'.
Scenario 2: Exploring a Pattern Based on Position
Another potential approach is to consider the position of each term in the sequence. Could the coefficient of 'z' be related to the term's position? The coefficients are 3, 2, and 5. This sequence doesn't immediately reveal an obvious pattern. It is not an arithmetic progression or a geometric progression.
Scenario 3: Considering Combinations and Operations
Let's examine if a specific operation applied repeatedly produces the sequence. For instance:
- Addition/Subtraction: Adding or subtracting a consistent value between terms doesn't seem to work.
- Multiplication/Division: Similarly, multiplication or division with a constant factor doesn't lead to a pattern for this sequence.
- More Complex Operations: It's also possible that the sequence involves more complex mathematical operations like exponentiation, logarithms, or modular arithmetic. This would require more extensive testing and investigation.
The Importance of Context and Additional Information
It's crucial to acknowledge that without additional context, there might be multiple valid solutions to this puzzle. The sequence, as presented, is open to interpretation. If this sequence came from a specific mathematical problem, a word problem, or a more extensive set of data, that additional information would greatly constrain the possible solutions and provide a clearer path to understanding the underlying logic.
Frequently Asked Questions (FAQ)
-
Q: Is there a single definitive answer to this sequence?
- A: Without additional context or constraints, it's unlikely there's a single definitive answer. Multiple mathematical relationships could potentially generate this sequence, depending on the assumptions made.
-
Q: What are some common pitfalls to avoid when solving sequences like this?
- A: Avoid jumping to conclusions too quickly. Systematically explore different approaches and document your findings. Be careful not to over-interpret patterns that might be coincidental.
-
Q: What resources could be used to solve more complex mathematical sequences?
- A: For more complex sequences, software such as mathematical modeling programs or programming languages (Python, MATLAB) can be extremely useful in testing various hypotheses and analyzing the results. Online resources and mathematical forums can also be valuable sources of information and collaboration.
Conclusion: The Value of Mathematical Exploration
The sequence "3z, 5, 2z, 25, 5z" serves as a compelling example of how a seemingly simple mathematical problem can spark creativity and critical thinking. While we haven't arrived at a single, definitive solution, the exploration process has highlighted various methods and approaches for deciphering mathematical sequences, demonstrating the importance of perseverance, methodical thinking, and the exploration of multiple pathways to a solution. The ambiguity of this sequence underscores the richness and flexibility within mathematics, encouraging further exploration and deeper understanding of mathematical principles. Remember, the journey of exploration is often just as valuable as finding the final answer. The analytical skills honed in addressing such problems are transferable to other areas of life, fostering a deeper appreciation for logic, reasoning, and problem-solving.
Latest Posts
Latest Posts
-
Cultural Heterosexism Is Characterized By
Sep 10, 2025
-
Which Nims Structure Makes Cooperative
Sep 10, 2025
-
Form The Tunica Externa Crossword
Sep 10, 2025
-
Formula For Copper I Carbonate
Sep 10, 2025
-
Cultural Psychology Steven J Heine
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3z 5 2z 25 5z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.