X 6 X 1 0
khabri
Sep 12, 2025 · 5 min read
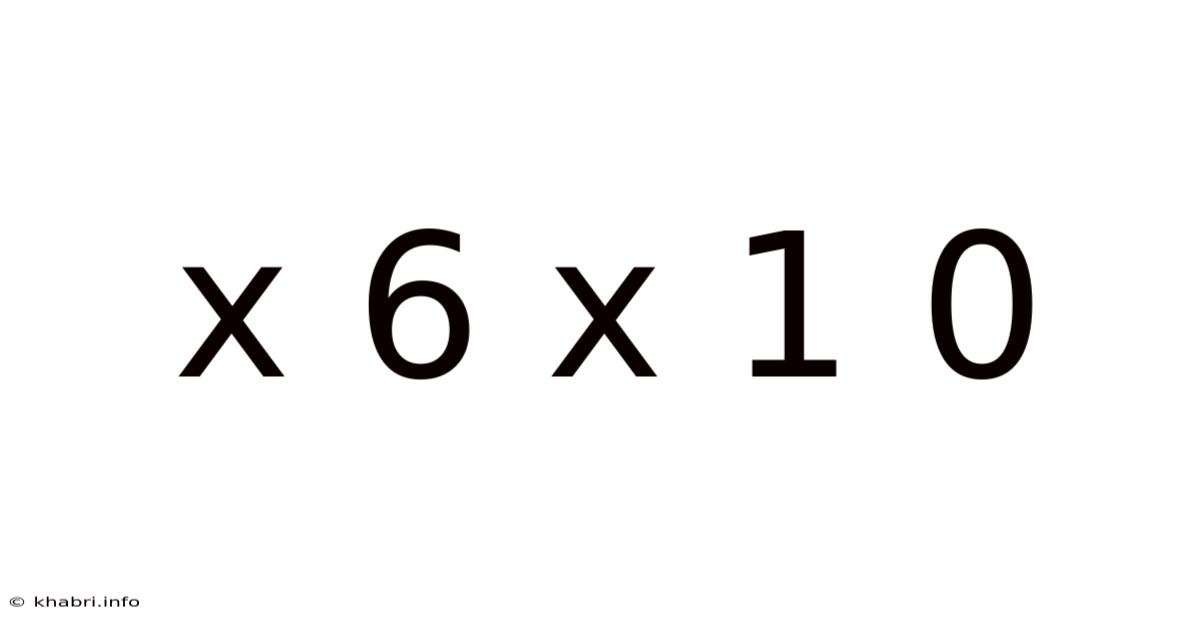
Table of Contents
Decoding the Mysterious X 6 X 10: Exploring Mathematical Concepts and Real-World Applications
This article delves into the intriguing mathematical expression "x 6 x 10," exploring its various interpretations, applications, and underlying mathematical principles. While seemingly simple at first glance, this expression opens doors to a wide range of mathematical concepts, from basic arithmetic to more advanced topics like algebra and even statistics. We'll unpack its meaning, explore its potential uses in different scenarios, and address common questions surrounding this expression. Understanding this seemingly simple expression will lay a strong foundation for further mathematical exploration.
Understanding the Basics: Order of Operations (PEMDAS/BODMAS)
Before we dive into the complexities (or lack thereof!), it's crucial to understand the order of operations. This dictates the sequence in which mathematical operations should be performed. The acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are commonly used. Both represent the same fundamental principle.
In our case, "x 6 x 10" involves only multiplication. Since multiplication is commutative (meaning the order doesn't affect the result; a x b = b x a), we can perform the operations in any order. However, understanding the order of operations is essential when dealing with more complex expressions involving different types of operations.
Interpreting "x 6 x 10": The Variable 'x'
The key to understanding "x 6 x 10" lies in the variable 'x'. In mathematics, a variable is a symbol (usually a letter) that represents an unknown quantity or a value that can change. This makes "x 6 x 10" not a fixed numerical value, but rather an algebraic expression. Its value depends entirely on the value assigned to 'x'.
Let's illustrate with examples:
- If x = 2: The expression becomes 2 x 6 x 10 = 120
- If x = 5: The expression becomes 5 x 6 x 10 = 300
- If x = 100: The expression becomes 100 x 6 x 10 = 6000
As you can see, the result varies significantly depending on the value of 'x'. This highlights the importance of understanding variables in mathematical expressions.
Applications of "x 6 x 10" and Similar Expressions
While "x 6 x 10" might seem abstract, expressions of this form have numerous applications in various fields:
-
Geometry: Imagine calculating the volume of a rectangular prism. If the length is 'x', the width is 6 units, and the height is 10 units, the volume would be given by x 6 x 10 cubic units. Substituting different values for 'x' (the length) would yield different volumes.
-
Physics: Many physics formulas involve multiplicative relationships between variables. For instance, calculating the force (F) required to accelerate a mass (m) at a certain acceleration (a) uses the formula F = m x a. If 'a' were consistently 6 m/s² and the mass were consistently 10 kg, then the force would simply be F = m x 6 x 10 Newtons. Different masses (m) would result in different forces.
-
Finance: Simple interest calculations involve multiplying the principal amount, the interest rate, and the time period. If the interest rate is 6% and the time period is 10 years, the total interest earned would be directly proportional to the principal amount ('x').
-
Data Analysis and Statistics: In statistical calculations, we often encounter expressions involving multiplication of variables and constants. For example, calculating a weighted average might involve multiplying each data point by a weight, then summing the products. A simplified scenario might use a constant weight of 6 for 10 data points, each represented by 'x'.
Expanding the Concept: Beyond Simple Multiplication
The expression "x 6 x 10" provides a foundation for understanding more complex algebraic concepts:
-
Linear Equations: We could transform "x 6 x 10" into a linear equation by setting it equal to a specific value. For example, x 6 x 10 = 180 becomes a linear equation that can be solved for 'x'.
-
Polynomials: If we were to add or subtract other terms involving 'x', we would create a polynomial. For instance, x 6 x 10 + 2x - 5 is a polynomial expression.
-
Functions: We can define a function, let's say f(x) = x 6 x 10, which takes a value of 'x' as input and returns the result of the calculation as output. This allows for a more formal mathematical representation and opens possibilities for analyzing the function's properties.
Solving for 'x': Techniques and Examples
To solve for 'x' in an equation involving "x 6 x 10", we use algebraic techniques:
Example 1: x 6 x 10 = 120
- Simplify: 60x = 120
- Isolate x: Divide both sides by 60: x = 120/60
- Solution: x = 2
Example 2: x 6 x 10 + 30 = 210
- Simplify: 60x + 30 = 210
- Isolate the x term: Subtract 30 from both sides: 60x = 180
- Isolate x: Divide both sides by 60: x = 180/60
- Solution: x = 3
These examples showcase the basic principles of solving algebraic equations, which is fundamental to many mathematical and scientific applications.
Frequently Asked Questions (FAQ)
Q1: What happens if 'x' is a negative number?
A1: The calculation remains the same. The result will simply be a negative number. For example, if x = -2, then x 6 x 10 = -120.
Q2: Can 'x' be a decimal or a fraction?
A2: Yes, absolutely. 'x' can represent any real number, including decimals and fractions. The calculation proceeds in the same manner.
Q3: What if there are more than just three terms involved in the multiplication, such as x * 6 * 10 * 2?
A3: The process is still the same. You would simply multiply all terms together: x * 6 * 10 * 2 = 120x.
Q4: How does this relate to more advanced mathematical concepts?
A4: "x 6 x 10" serves as a building block for understanding more complex concepts like linear algebra, calculus, and even abstract algebra. The ability to manipulate algebraic expressions is foundational to these advanced fields.
Conclusion: The Significance of Simple Expressions
The seemingly simple expression "x 6 x 10" provides a valuable entry point into the world of algebra and its numerous applications. By understanding variables, order of operations, and basic algebraic manipulation, we can unlock the potential of this expression and apply these principles to various real-world problems. While seemingly straightforward, this expression offers a springboard to more advanced mathematical concepts, highlighting the fundamental importance of grasping even the simplest mathematical building blocks. The ability to interpret, manipulate, and solve expressions like this forms the bedrock of mathematical literacy and problem-solving skills.
Latest Posts
Latest Posts
-
Vanders Human Physiology 16th Edition
Sep 12, 2025
-
Professional Nursing Concepts And Challenges
Sep 12, 2025
-
Cd4 Markers Are Found On
Sep 12, 2025
-
Identify The Structure Labeled D
Sep 12, 2025
-
Lewis Structure For Ch3 3coh
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 6 X 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.