X 3 X 4 8
khabri
Sep 15, 2025 · 6 min read
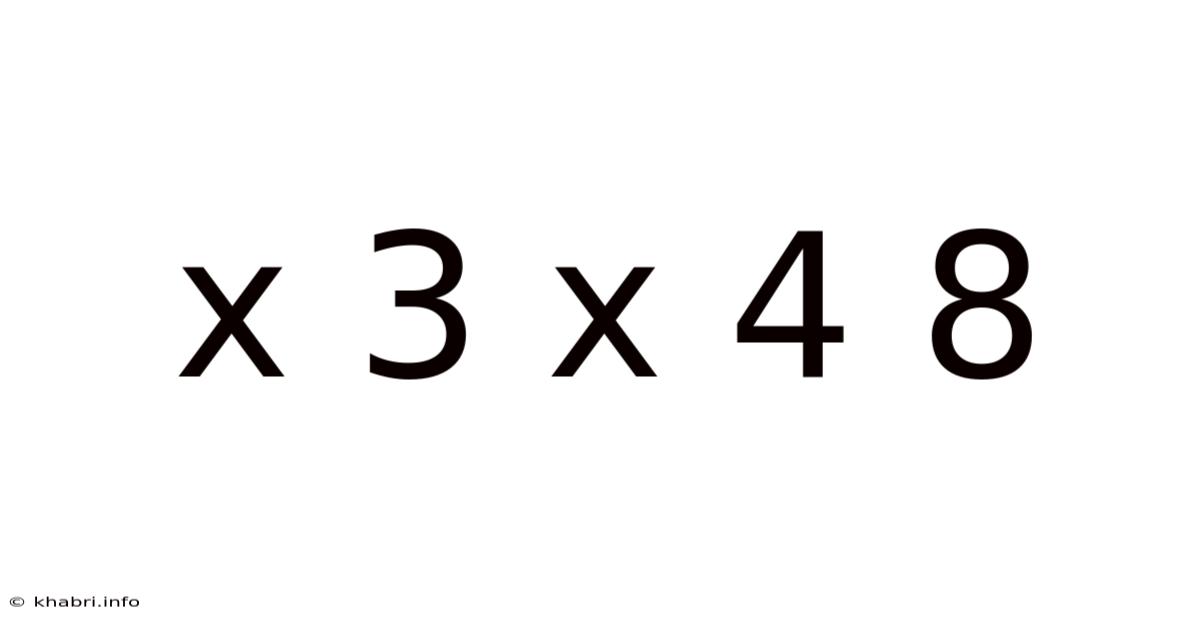
Table of Contents
Decoding the Mystery: Exploring the Mathematical and Conceptual Aspects of "x 3 x 4 = 8"
This seemingly simple equation, "x 3 x 4 = 8," immediately presents a challenge. It's not a standard algebraic equation with a single, readily apparent solution. Instead, it opens a door to exploring various mathematical concepts, problem-solving strategies, and even interpretations beyond traditional arithmetic. This article will delve into the multiple layers of understanding embedded within this intriguing expression, moving from basic arithmetic to more complex mathematical concepts and potential ambiguities. We will explore different approaches to solving this puzzle and discuss its implications for mathematical reasoning.
Understanding the Problem: Beyond Simple Multiplication
At first glance, "x 3 x 4 = 8" looks like a straightforward multiplication problem. We might instinctively attempt to solve it by dividing 8 by 12 (3 x 4), resulting in a fractional answer (2/3). However, this approach ignores the potential complexities and nuances of the problem statement. The crucial element lies in interpreting the "x" and understanding its possible roles. It's not just a variable representing an unknown number; it could signify an operation, a placeholder, or even an element within a more elaborate system.
Possible Interpretations and Solutions
Let's explore some potential interpretations of "x" and how they lead to different solutions:
1. "x" as a Standard Variable:
If we assume "x" is a standard algebraic variable representing an unknown number, then the equation becomes:
x * 3 * 4 = 8
Solving for x:
12x = 8 x = 8/12 x = 2/3
This is the most straightforward interpretation, yielding a fractional solution. This approach applies standard algebraic principles.
2. "x" as a Placeholder for an Operation:
Here, "x" doesn't represent a number but a mathematical operation. This introduces a far greater degree of complexity and multiple possibilities. For example:
-
"x" representing subtraction: Let's assume "x" signifies subtraction. This could lead to various possibilities depending on the order of operations. One possibility is: (8 - 3) - 4, which would equal 1, or other arrangements depending on how we use the subtraction operation within the expression.
-
"x" representing division: Similarly, if we interpret "x" as division, numerous combinations might satisfy the equation, depending on the placement of the division operation and the order of operations.
-
"x" representing exponentiation: Could "x" represent an exponent? For example, if the equation were rewritten as (x³) * 4 = 8, then solving for x would require a different mathematical approach involving cube roots.
3. "x" within a Modular Arithmetic System:
Modular arithmetic involves performing arithmetic operations within a specific modulus, or a remainder after division by a specific number. Consider a modulus of 4. In this system, any number that is a multiple of 4 is considered to be 0. Then, within this modulus 4, the equation could be considered a possibility within specific constraints. This approach requires a sophisticated understanding of modular arithmetic.
4. "x" in a More Complex Mathematical System:
Beyond standard arithmetic and modular arithmetic, "x" could represent an operator or element within more complex mathematical systems like matrix algebra or abstract algebra. These systems involve advanced mathematical concepts far beyond the scope of a basic equation.
Exploring Problem-Solving Strategies
The lack of a clear, single solution necessitates the adoption of varied problem-solving strategies. These might include:
-
Trial and Error: Experimenting with different values for "x" or different interpretations of the equation could potentially reveal a solution within a specific context. This approach is less rigorous but can lead to valuable insights.
-
Systematic Approach: A more structured approach would involve listing potential interpretations of "x" and systematically testing each interpretation to see if it results in a valid solution. This provides a more organized approach to exploring the problem space.
-
Working Backwards: Instead of solving for "x" directly, consider starting from the result (8) and working backward to determine possible input values and interpretations of the equation that would lead to 8 as a result.
-
Utilizing Symbolic Logic: In certain interpretations, using symbolic logic could be valuable in clearly outlining the different operations and finding a solution.
The Importance of Context and Clarity in Mathematics
The ambiguity of "x 3 x 4 = 8" highlights the critical importance of context and precise notation in mathematics. Without clear definitions of what "x" represents and the order of operations, the equation becomes ill-defined. This underscores the need for precision in mathematical communication and problem statements.
Mathematical Reasoning and Critical Thinking
This seemingly simple problem acts as a valuable exercise in mathematical reasoning and critical thinking. It encourages us to move beyond rote memorization and formula application to consider multiple perspectives and interpret the problem creatively. The lack of a single, obvious solution requires us to carefully consider the possibilities, systematically explore the options, and justify our conclusions, all of which are crucial skills in problem-solving and mathematical thinking.
Frequently Asked Questions (FAQ)
Q: Is there one correct answer to "x 3 x 4 = 8"?
A: No, there isn't a single correct answer without further clarifying the meaning of "x" and the implied order of operations. The equation is deliberately ambiguous to highlight the importance of clear notation and contextual understanding in mathematics.
Q: What mathematical concepts are relevant to solving this type of problem?
A: This problem touches upon various concepts, including basic arithmetic, algebraic manipulation, order of operations (PEMDAS/BODMAS), modular arithmetic, and more advanced concepts like abstract algebra (depending on the interpretation of "x").
Q: How can this problem be used in education?
A: This problem serves as an excellent tool for engaging students in critical thinking and problem-solving. It encourages them to explore multiple approaches, justify their reasoning, and appreciate the importance of precise mathematical communication. It promotes a deeper understanding of the underlying principles rather than simply memorizing procedures.
Conclusion: Embracing Ambiguity and the Power of Interpretation
"x 3 x 4 = 8" isn't simply a failed mathematical equation; it's a fascinating puzzle that challenges our assumptions and expands our understanding of mathematical principles. The ambiguity embedded within the problem encourages creative thinking, problem-solving skills, and an appreciation for the importance of clear communication in mathematics. Instead of searching for one definitive answer, embrace the multiple interpretations and solutions. This exploration demonstrates how seemingly simple problems can unlock profound insights into the nature of mathematics and the power of human interpretation. By grappling with this ambiguous equation, we cultivate a deeper and more nuanced understanding of the mathematical world. It's a reminder that mathematics is not just about finding answers, but also about asking the right questions and exploring the possibilities that arise from ambiguous situations. The journey of understanding, more than the destination, is often the most valuable part of the learning experience.
Latest Posts
Latest Posts
-
Materializing Motivation Through Strategic Hr
Sep 15, 2025
-
Socially Or Economically Disadvantaged Subjects
Sep 15, 2025
-
Discrete Time Fourier Transform Table
Sep 15, 2025
-
What Is True About Vechainthor
Sep 15, 2025
-
Vive La France Math Worksheet
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.