X 3 Ln X Integral
khabri
Sep 12, 2025 · 6 min read
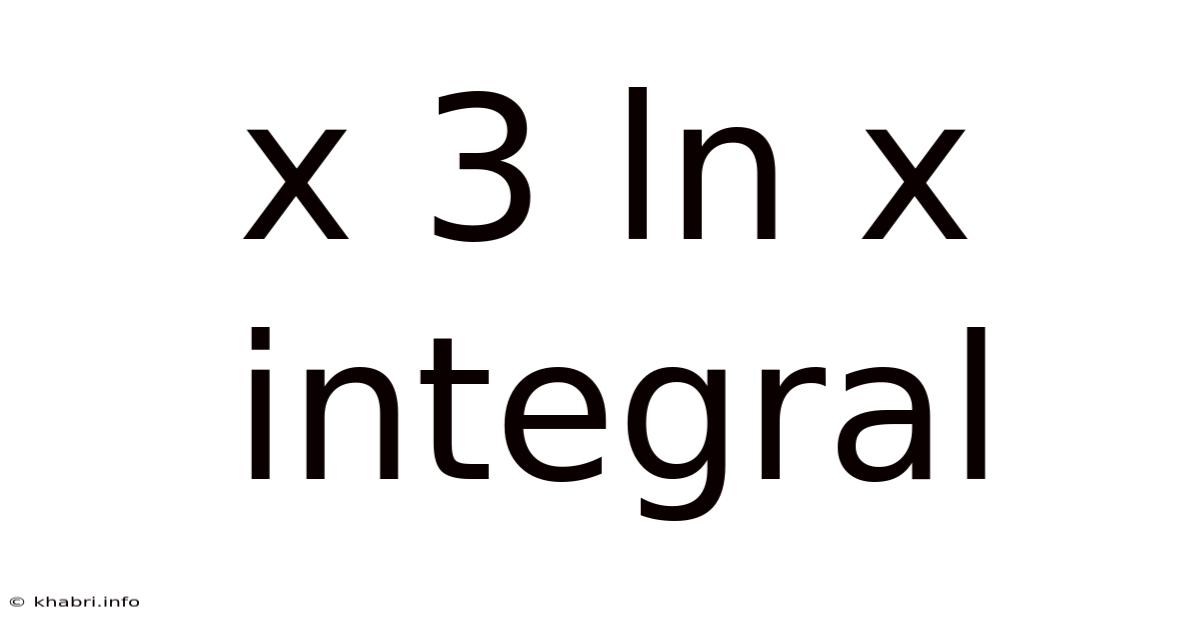
Table of Contents
Solving the Definite Integral of x³ln(x)
The definite integral ∫x³ln(x) dx presents a seemingly complex challenge, but with the right approach, it becomes manageable. This comprehensive guide will walk you through the solution, explaining each step in detail and offering insights into the underlying mathematical concepts. We will explore various techniques, delve into the underlying theory, and address frequently asked questions. This will equip you not just with the solution, but also a deeper understanding of integration techniques applicable to a broader range of problems.
Introduction: Understanding the Problem
The integral ∫x³ln(x) dx involves a product of two functions: a power function, x³, and a logarithmic function, ln(x). Direct integration isn't straightforward; we need a technique that handles such products effectively. This is where integration by parts comes into play. This article will focus primarily on solving the indefinite integral, but understanding this is crucial before tackling any definite integrals with specific limits.
Integration by Parts: The Key Technique
Integration by parts is a powerful technique derived from the product rule of differentiation. It states:
∫u dv = uv - ∫v du
Where 'u' and 'v' are functions of x. The success of this method hinges on choosing 'u' and 'dv' strategically. A common mnemonic device is "LIATE," prioritizing functions in the following order for 'u':
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (polynomials like x³)
- Trigonometric functions
- Exponential functions
Step-by-Step Solution: Applying Integration by Parts
Let's apply integration by parts to ∫x³ln(x) dx.
-
Choosing u and dv: Following LIATE, we choose:
- u = ln(x) => du = (1/x) dx
- dv = x³ dx => v = (1/4)x⁴
-
Applying the Formula: Substitute these values into the integration by parts formula:
∫x³ln(x) dx = (ln(x)) dx
-
Simplifying: Simplify the resulting integral:
∫x³ln(x) dx = (1/4)x⁴ln(x) - (1/4)∫x³ dx
-
Integrating the Remaining Term: Integrate the simplified term:
∫x³ dx = (1/4)x⁴
-
Combining and Adding the Constant of Integration: Combine the terms and remember to add the constant of integration, 'C', which represents all possible constants that could result from the integration:
∫x³ln(x) dx = (1/4)x⁴ln(x) - (1/16)x⁴ + C
Verification Through Differentiation
A crucial step in verifying the correctness of any integration is to differentiate the result. If the derivative matches the original integrand, our solution is accurate. Let's differentiate our solution:
d/dx [(1/4)x⁴ln(x) - (1/16)x⁴ + C] = x³ln(x) + (1/4)x⁴(1/x) - (1/4)x³ = x³ln(x) + (1/4)x³ - (1/4)x³ = x³ln(x)
The derivative matches the original integrand, confirming the accuracy of our integration.
Definite Integrals: Applying Limits of Integration
To solve a definite integral, we need to evaluate the indefinite integral at the upper and lower limits of integration and subtract the results. Let's consider the example:
∫[from a to b] x³ln(x) dx
-
Evaluate the indefinite integral: We already have the indefinite integral: (1/4)x⁴ln(x) - (1/16)x⁴ + C
-
Substitute the limits: Substitute the upper limit 'b' and lower limit 'a' into the indefinite integral:
[(1/4)b⁴ln(b) - (1/16)b⁴] - [(1/4)a⁴ln(a) - (1/16)a⁴]
-
Simplify: This expression represents the exact value of the definite integral. Further simplification might be possible depending on the values of 'a' and 'b'. Remember that 'a' must be greater than 0 because ln(x) is undefined for x ≤ 0.
Dealing with Different Power Functions
The method outlined above can be extended to integrals of the form ∫xⁿln(x) dx, where 'n' is any real number except -1. The steps remain the same:
-
Choose u and dv: Let u = ln(x) and dv = xⁿ dx.
-
Find du and v: du = (1/x) dx and v = xⁿ⁺¹/(n+1)
-
Apply Integration by Parts: Follow the integration by parts formula.
-
Simplify and Integrate: Simplify the resulting expression and integrate the remaining term.
-
Add the Constant of Integration (for indefinite integrals): Remember to include 'C' for indefinite integrals.
Handling More Complex Integrals
The fundamental principle of integration by parts remains consistent even with more intricate integrands involving products of logarithmic and other functions. The key is to strategically choose 'u' and 'dv' to simplify the integral. Sometimes, you might need to apply integration by parts multiple times to solve more complex problems.
Further Exploration: Applications and Extensions
The integral of x³ln(x) and its generalizations find applications in various fields, including:
- Probability and Statistics: In probability density functions and moment calculations.
- Physics: Solving differential equations related to growth and decay processes.
- Engineering: In modeling and analyzing systems involving logarithmic relationships.
The techniques demonstrated here can be adapted and expanded upon to tackle more challenging integrals.
Frequently Asked Questions (FAQ)
Q1: What happens if the lower limit of integration is 0 or negative?
A1: The natural logarithm, ln(x), is undefined for x ≤ 0. Therefore, definite integrals involving ln(x) must have lower limits greater than 0.
Q2: Can I use other integration techniques besides integration by parts?
A2: For this specific integral, integration by parts is the most efficient and straightforward approach. Other techniques might be less effective or require more complex manipulations.
Q3: What if the integrand contains a more complex function than x³?
A3: The same principles apply. You would choose 'u' and 'dv' appropriately based on the LIATE rule and apply integration by parts repeatedly if necessary.
Q4: Are there any limitations to integration by parts?
A4: While powerful, integration by parts might not always lead to a simple, closed-form solution. Some integrals require advanced techniques or might not have elementary solutions.
Q5: How can I improve my skills in solving integrals?
A5: Practice is key! Work through various examples of increasing difficulty. Focus on understanding the underlying concepts rather than rote memorization of formulas. Consult textbooks and online resources to broaden your understanding and explore different approaches.
Conclusion: Mastering the Integral
Solving the integral ∫x³ln(x) dx effectively involves a structured application of integration by parts. Understanding this technique provides a foundation for tackling a wide range of integration problems involving products of functions. Remember to choose 'u' and 'dv' strategically, carefully apply the formula, and always verify your solution through differentiation. The ability to solve such integrals is crucial for success in advanced mathematics, engineering, and scientific disciplines. This comprehensive guide offers not only the solution but also a deeper understanding of the concepts and techniques involved, empowering you to approach similar challenges with confidence. By diligently practicing and understanding the underlying principles, you'll significantly enhance your mathematical problem-solving capabilities.
Latest Posts
Latest Posts
-
Molecular Orbital Diagram For Ne2
Sep 12, 2025
-
Corporate Financing Comes Ultimately From
Sep 12, 2025
-
Molecular Orbital Diagram Of Hcl
Sep 12, 2025
-
Convert 8 Bit To 7 Bit
Sep 12, 2025
-
Cavity Surrounded By The Skull
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 3 Ln X Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.