X 2 2x 2 0
khabri
Sep 14, 2025 · 6 min read
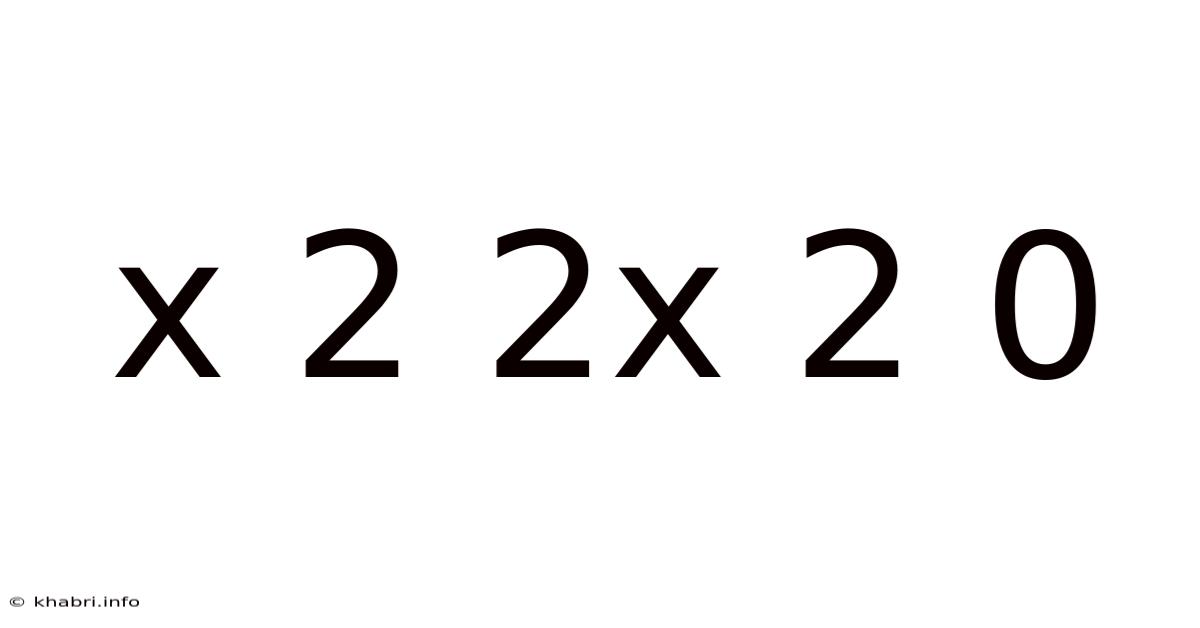
Table of Contents
Decoding the Enigma: A Deep Dive into x² - 2x + 2 = 0
This article explores the quadratic equation x² - 2x + 2 = 0, delving into its solution, its graphical representation, and its broader implications within the field of algebra. We'll uncover its fascinating properties and demonstrate how to solve it using various methods, making this seemingly simple equation a gateway to understanding more complex mathematical concepts. Understanding this equation provides a strong foundation in solving quadratic equations and appreciating their applications in diverse fields.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. It takes the general form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero. Our specific equation, x² - 2x + 2 = 0, fits this mold with a = 1, b = -2, and c = 2. Solving this equation means finding the values of 'x' that make the equation true. These values are known as the roots or solutions of the equation.
Method 1: The Quadratic Formula – A Universal Solution
The quadratic formula is a powerful tool for solving any quadratic equation. It provides a direct way to calculate the roots, regardless of whether the equation can be easily factored. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = -2, c = 2) into the quadratic formula, we get:
x = [2 ± √((-2)² - 4 * 1 * 2)] / (2 * 1) x = [2 ± √(4 - 8)] / 2 x = [2 ± √(-4)] / 2
Notice that we have the square root of a negative number, √(-4). This indicates that the roots of this equation are complex numbers.
Understanding Complex Numbers
Complex numbers are numbers that contain both a real part and an imaginary part. The imaginary unit, denoted by 'i', is defined as √(-1). Therefore, √(-4) can be rewritten as √(4 * -1) = 2i. Our equation's solutions now become:
x = [2 ± 2i] / 2 x = 1 ± i
Therefore, the two roots of the equation x² - 2x + 2 = 0 are x = 1 + i and x = 1 - i. These are complex conjugate pairs, a common characteristic of quadratic equations with no real roots.
Method 2: Completing the Square – A Geometric Approach
Completing the square is another valuable method for solving quadratic equations. It involves manipulating the equation to form a perfect square trinomial, which can then be easily factored. Let's apply this method to our equation:
x² - 2x + 2 = 0
-
Move the constant term to the right side: x² - 2x = -2
-
Take half of the coefficient of 'x' (-2), square it ((-1)² = 1), and add it to both sides: x² - 2x + 1 = -2 + 1 x² - 2x + 1 = -1
-
Factor the left side as a perfect square: (x - 1)² = -1
-
Take the square root of both sides: x - 1 = ±√(-1) x - 1 = ±i
-
Solve for 'x': x = 1 ± i
This method confirms our previous result: the roots are x = 1 + i and x = 1 - i. Completing the square offers a deeper understanding of the equation's structure and is particularly useful for deriving the quadratic formula itself.
Method 3: Graphical Representation – Visualizing the Roots
Graphing the quadratic equation y = x² - 2x + 2 provides a visual representation of its behavior and helps us understand why it has no real roots. The parabola represented by this equation does not intersect the x-axis, meaning there are no real values of 'x' for which y = 0. The parabola's vertex can be found using the formula x = -b/2a = 2/2 = 1. When x = 1, y = 1² - 2(1) + 2 = 1. Therefore, the vertex of the parabola is at (1, 1). Since the parabola opens upwards (because 'a' is positive), it lies entirely above the x-axis, confirming that there are no real roots. The complex roots represent the points where the parabola would intersect the x-axis if we were to extend the graph into the complex plane.
The Discriminant: Predicting the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. It plays a crucial role in determining the nature of the roots:
- b² - 4ac > 0: Two distinct real roots. The parabola intersects the x-axis at two different points.
- b² - 4ac = 0: One real root (a repeated root). The parabola touches the x-axis at one point.
- b² - 4ac < 0: Two complex conjugate roots. The parabola does not intersect the x-axis.
In our equation, the discriminant is (-2)² - 4(1)(2) = -4, which is less than 0, confirming the presence of two complex conjugate roots.
Applications of Quadratic Equations
Quadratic equations find wide applications across various fields. Some notable examples include:
- Physics: Calculating projectile motion, determining the trajectory of an object under gravity.
- Engineering: Designing structures, calculating optimal dimensions for beams and supports.
- Economics: Modeling supply and demand curves, analyzing market equilibrium.
- Computer graphics: Generating curves and shapes, modeling three-dimensional objects.
Frequently Asked Questions (FAQ)
Q1: Why are complex numbers important in solving this equation?
A1: Complex numbers extend the number system beyond real numbers, enabling us to find solutions for equations that have no real roots. Our equation represents a case where the parabola doesn't intersect the x-axis in the real plane, but its intersections exist in the complex plane.
Q2: Can any quadratic equation be solved using the quadratic formula?
A2: Yes, the quadratic formula is a universal method for solving any quadratic equation, regardless of the nature of its roots (real or complex).
Q3: What is the significance of the discriminant?
A3: The discriminant quickly tells us the type of roots a quadratic equation possesses—real and distinct, real and equal, or complex conjugate pairs—without actually solving the equation.
Q4: Is there a geometrical interpretation of complex roots?
A4: While not directly visible on a standard Cartesian plane, complex roots can be visualized on a complex plane (Argand plane), where the real part is plotted along the x-axis and the imaginary part along the y-axis. The complex roots represent points on this plane.
Q5: Can I solve this equation using factorization?
A5: While the quadratic formula and completing the square work perfectly, factorization is not directly applicable to this particular equation because it doesn't factor neatly into real numbers.
Conclusion: A Deeper Appreciation of Quadratic Equations
The seemingly simple equation x² - 2x + 2 = 0 offers a rich exploration into the world of quadratic equations and complex numbers. By applying different solution methods, we've not only found its roots but also gained a deeper understanding of their nature. The concepts discussed here—the quadratic formula, completing the square, the discriminant, and the graphical representation—are fundamental tools in algebra and have far-reaching applications in numerous fields. Mastering these concepts is crucial for anyone pursuing further studies in mathematics and related disciplines. The journey of understanding this equation serves as a springboard to tackle more complex mathematical challenges. Remember, even seemingly simple equations can unlock a world of fascinating mathematical insights.
Latest Posts
Latest Posts
-
Identifying Hydrogen Bonding Interactions Between Molecules
Sep 14, 2025
-
Lewis Dot Structure For Asf3
Sep 14, 2025
-
Active Learning Template Nursing Skill
Sep 14, 2025
-
Public Budgeting Systems 10th Edition
Sep 14, 2025
-
Mla Citation Of A Letter
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.