What Times -80 Equals -40
khabri
Sep 06, 2025 · 6 min read
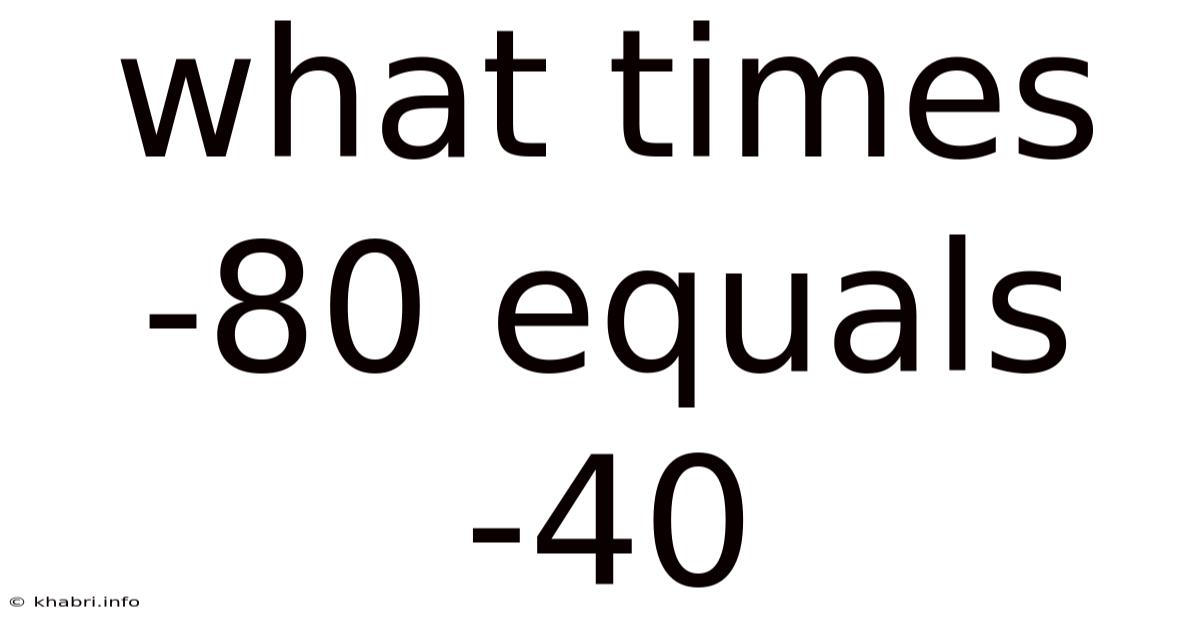
Table of Contents
What Times -80 Equals -40? Understanding Multiplication with Negative Numbers
This article explores the seemingly simple question: "What times -80 equals -40?" While the answer might seem immediately obvious to some, delving into the problem reveals a deeper understanding of multiplication with negative numbers, a crucial concept in mathematics. We'll unravel the solution, explore the underlying principles, and examine related concepts to build a comprehensive understanding. This will include a look at the properties of multiplication, the concept of reciprocals, and practical applications of these mathematical concepts.
Introduction: The Basics of Multiplication
Before tackling the specific problem, let's refresh our understanding of multiplication. Multiplication is essentially repeated addition. For instance, 3 x 4 means adding 3 four times: 3 + 3 + 3 + 3 = 12. This basic understanding forms the foundation for working with both positive and negative numbers.
When multiplying positive numbers, the result is always positive. However, when negative numbers are involved, the rules become slightly more complex, but still logically consistent.
Solving the Equation: What Times -80 Equals -40?
The question, "What times -80 equals -40?" can be represented algebraically as:
x * -80 = -40
To solve for x, we need to isolate x on one side of the equation. We can do this by dividing both sides of the equation by -80:
x = -40 / -80
Dividing a negative number by a negative number results in a positive number. Therefore:
x = 1/2 or x = 0.5
Therefore, one-half times -80 equals -40.
Understanding the Rules of Multiplication with Negative Numbers
The rules for multiplying numbers with different signs are as follows:
-
Positive x Positive = Positive: A positive number multiplied by a positive number always results in a positive number. (e.g., 5 x 3 = 15)
-
Positive x Negative = Negative: A positive number multiplied by a negative number always results in a negative number. (e.g., 5 x -3 = -15)
-
Negative x Positive = Negative: A negative number multiplied by a positive number always results in a negative number. (e.g., -5 x 3 = -15)
-
Negative x Negative = Positive: This is often the most challenging rule to grasp. A negative number multiplied by a negative number always results in a positive number. (e.g., -5 x -3 = 15)
The reason behind the "negative times negative equals positive" rule is best understood conceptually. Consider the concept of multiplication as scaling. Multiplying by a positive number scales the number in the same direction; multiplying by a negative number scales the number in the opposite direction. Therefore, multiplying by two negative numbers effectively reverses the direction twice, resulting in a positive outcome.
The Concept of Reciprocals
In our equation, we used division to solve for x. Division and multiplication are inversely related. The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 2 is 1/2.
- The reciprocal of -80 is -1/80.
Understanding reciprocals is crucial because multiplying a number by its reciprocal always equals 1 (except for 0, which has no reciprocal). This concept is useful in various mathematical operations, including solving equations. In our case, we essentially found the reciprocal of -80 (which is -1/80) and multiplied it by -40 to solve for x.
Practical Applications: Real-World Examples
The concepts explored here are not just abstract mathematical ideas. They have numerous practical applications in various fields:
-
Finance: Calculating profit and loss, managing debts (negative numbers representing debts), and understanding interest rates all involve multiplication with negative numbers. For instance, a loss of $80 per transaction, resulting in a total loss of $40, means only 0.5 transaction happened.
-
Physics: In physics, vectors often have both magnitude and direction. Negative numbers are used to represent direction (e.g., negative velocity indicating movement in the opposite direction). Calculations involving vectors frequently utilize multiplication with negative numbers.
-
Computer Science: Programming relies heavily on mathematics, and understanding multiplication with negative numbers is essential for manipulating data, handling errors, and optimizing algorithms. For example, in game development, negative numbers might represent movement in a specific direction.
-
Engineering: In various engineering fields, from civil to electrical, calculations often involve negative values representing quantities like force, pressure or voltage in opposite directions. Accurate calculations depend heavily on a strong grasp of the rules governing multiplication of negative numbers.
Further Exploration: Extending the Concepts
The principles discussed here provide a solid foundation for understanding more complex mathematical concepts involving negative numbers:
-
Exponents: When dealing with negative numbers raised to powers, the rules of multiplication with negative numbers still apply. Remember that an even exponent leads to a positive result, while an odd exponent preserves the original sign.
-
Algebra: Solving algebraic equations frequently requires manipulating negative numbers. Understanding how to work with them is fundamental to proficiency in algebra.
-
Calculus: Calculus builds upon algebraic concepts, and mastery of negative numbers is critical for understanding derivatives and integrals.
-
Linear Algebra: The concept of multiplying matrices and vectors can involve negative numbers, making the understanding of their multiplication essential for this subject.
Frequently Asked Questions (FAQ)
Q: Why is negative times negative positive?
A: While there are various ways to explain this, a conceptual approach is helpful. Think of multiplication as scaling and direction. A negative sign indicates a change in direction. Multiplying by two negatives is like changing direction twice, resulting in a return to the original direction (positive).
Q: Can I use a calculator to solve this kind of problem?
A: Yes, absolutely. Calculators are excellent tools for checking your work and handling more complex calculations involving negative numbers. However, it's important to understand the underlying principles, as calculators alone won't help you fully grasp the concepts.
Q: What if the numbers were larger or involved decimals?
A: The principles remain the same. Regardless of the size or type of number (integer, decimal, fraction), the rules for multiplying positive and negative numbers still apply. However, for complex numbers, the process might involve using algebraic techniques or calculators.
Conclusion: Mastering Multiplication with Negative Numbers
Understanding multiplication with negative numbers is a cornerstone of mathematical proficiency. While the rules might initially seem counterintuitive, they are consistent and logical. By grasping the underlying principles, including the concept of reciprocals and the relationship between multiplication and division, you'll build a strong foundation for tackling more advanced mathematical concepts. The ability to work confidently with negative numbers is essential for success in various fields, from finance and science to computer science and engineering. Remember that practice is key – the more you work with these rules, the more intuitive they will become. Don't be afraid to experiment, ask questions, and explore related concepts to solidify your understanding.
Latest Posts
Latest Posts
-
A Nucleotide Does Not Contain
Sep 07, 2025
-
Stress Strain Curve Aluminum 6061
Sep 07, 2025
-
Four Components Of Aggregate Demand
Sep 07, 2025
-
Norton Field Guide To Speaking
Sep 07, 2025
-
Mona Works At A Bank
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Times -80 Equals -40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.