What Is 3 X 2
khabri
Sep 08, 2025 · 6 min read
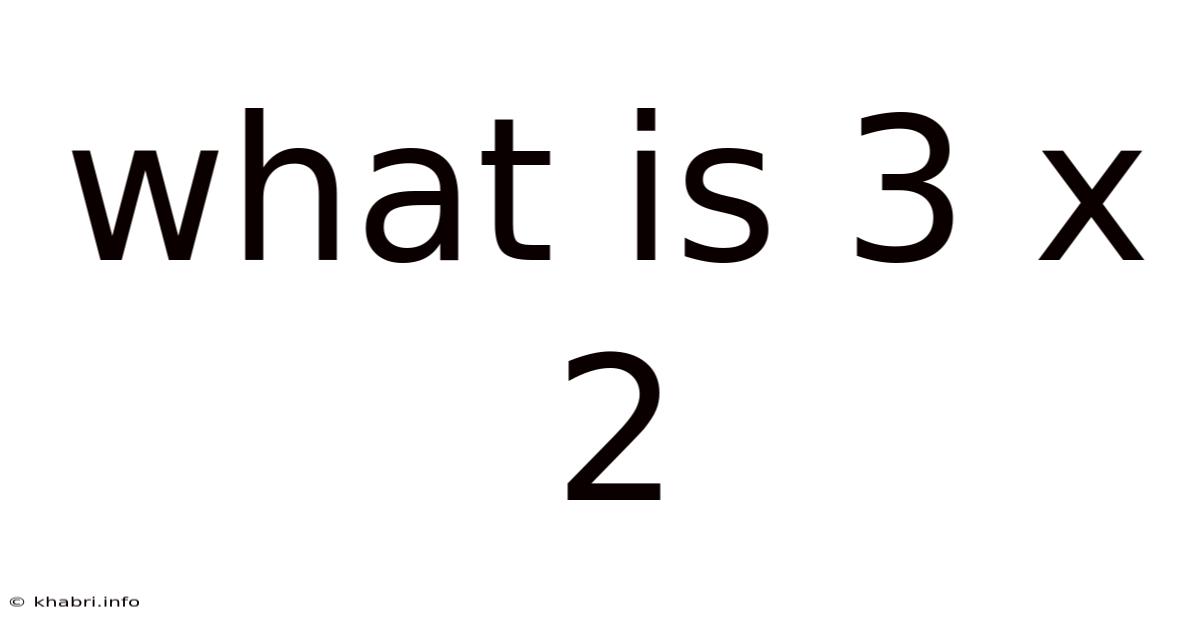
Table of Contents
Decoding 3 x 2: A Deep Dive into Multiplication
What is 3 x 2? At first glance, this seems like a trivially simple question, suitable only for the youngest of learners. However, this seemingly basic arithmetic problem opens a door to a much deeper understanding of mathematics, encompassing fundamental concepts, practical applications, and the beauty of numerical relationships. This article will explore 3 x 2 from multiple perspectives, delving into its meaning, its calculation, its representation, and its broader implications within the world of mathematics and beyond. We'll also explore some frequently asked questions and uncover the surprising depth hidden within this seemingly simple equation.
Understanding Multiplication: The Foundation
Before we tackle 3 x 2 specifically, let's establish a solid understanding of multiplication itself. Multiplication is essentially a shorthand for repeated addition. It's a way of efficiently calculating the total when you have multiple groups of the same size. For example, 3 x 2 means adding the number 2 three times: 2 + 2 + 2 = 6. This fundamental concept applies across all multiplication problems, making it the cornerstone of arithmetic and beyond.
We can visualize this concept in various ways. Imagine three bags, each containing two apples. To find the total number of apples, we can either count each apple individually or use multiplication: 3 bags × 2 apples/bag = 6 apples. This simple example illustrates the practical application of multiplication in everyday life.
Calculating 3 x 2: Different Approaches
While the answer to 3 x 2 is clearly 6, let's explore several ways to arrive at this answer, emphasizing different aspects of mathematical thinking:
-
Repeated Addition: As mentioned earlier, this is the most fundamental approach. We simply add the number 2 three times: 2 + 2 + 2 = 6. This method is visually intuitive and helps build a strong conceptual understanding of multiplication.
-
Using a Number Line: A number line provides a visual representation of the operation. Starting at 0, we move two units to the right three times, ending up at 6. This method reinforces the connection between addition and multiplication.
-
Multiplication Table: The multiplication table is a tool that memorizes the products of common numbers. Looking up 3 x 2 in a multiplication table instantly provides the answer, 6. This approach emphasizes rote memorization, which can be helpful for quick calculations, but it’s crucial to understand the underlying principle.
-
Array Model: We can visually represent 3 x 2 as a rectangular array with three rows and two columns. By counting the total number of squares in the array, we arrive at the answer 6. This method is particularly helpful for visualizing the commutative property of multiplication (more on this later).
The Commutative Property and its Significance
The commutative property of multiplication states that the order of the numbers being multiplied does not affect the result. In simpler terms, 3 x 2 is the same as 2 x 3. Both operations yield the same answer: 6. This property is not only true for 3 x 2 but for all multiplication problems. Understanding this property helps simplify calculations and fosters a deeper understanding of the structure of mathematics.
We can visualize this using the array model. A 3 x 2 array is simply a rotated version of a 2 x 3 array; the total number of squares remains the same. This illustrates the inherent symmetry within the operation of multiplication. This commutative property is fundamental and extends beyond simple arithmetic, playing a critical role in more advanced mathematical concepts.
3 x 2 in Different Number Systems
While we've focused on the decimal system (base 10), let's briefly explore how 3 x 2 is represented and calculated in other number systems:
-
Binary (base 2): In binary, 3 is represented as 11 and 2 as 10. The multiplication process would involve binary addition and shifting, resulting in 110, which is equivalent to 6 in decimal.
-
Hexadecimal (base 16): In hexadecimal, 3 and 2 remain the same. 3 x 2 = 6, which is also 6 in hexadecimal.
This shows that the fundamental relationship between 3 and 2, and their product 6, transcends different number systems. The underlying mathematical principle remains consistent despite changes in representation.
Applications of 3 x 2 in Real-World Scenarios
While seemingly simple, the concept of 3 x 2 finds applications in countless real-world scenarios:
-
Shopping: Buying three items at $2 each.
-
Baking: Using three cups of flour, with each cup containing two tablespoons of baking powder.
-
Construction: Arranging three rows of bricks with two bricks in each row.
-
Gardening: Planting three rows of flowers with two flowers in each row.
These are just a few examples showcasing how this fundamental multiplication problem permeates our daily lives.
Extending the Concept: Beyond 3 x 2
Understanding 3 x 2 serves as a springboard to explore more complex mathematical concepts:
-
Algebra: The principles of multiplication extend to algebraic expressions, where variables replace numbers. For instance, 3x = 6, where x represents 2.
-
Geometry: Calculating the area of a rectangle with dimensions 3 units by 2 units.
-
Calculus: Multiplication forms the basis for various calculus operations, including differentiation and integration.
-
Higher Mathematics: The concept of multiplication underlies numerous sophisticated mathematical concepts and theorems across various branches of mathematics.
Frequently Asked Questions (FAQ)
Q: Is 3 x 2 the same as 2 x 3?
A: Yes, due to the commutative property of multiplication, 3 x 2 and 2 x 3 are equivalent and both equal 6.
Q: What is the opposite of multiplication?
A: The opposite of multiplication is division. Just as 3 x 2 = 6, 6 ÷ 2 = 3 and 6 ÷ 3 = 2.
Q: Why is multiplication important?
A: Multiplication is a fundamental arithmetic operation used for efficient calculations and solving various problems in everyday life, science, engineering, and finance. It streamlines calculations, allowing for efficient problem-solving in numerous fields.
Q: Can multiplication be visualized in other ways besides arrays?
A: Yes, other visual aids include tree diagrams, area models, and using objects like counters or blocks to create groups. Each approach offers a slightly different way to understand the concept of repeated addition.
Conclusion: The Enduring Power of Simplicity
The seemingly simple equation 3 x 2 = 6 holds a wealth of mathematical depth. From its fundamental role in repeated addition to its applications in advanced mathematics and real-world scenarios, this equation highlights the interconnectedness of mathematical concepts. Understanding this basic multiplication problem provides a solid foundation for more advanced mathematical explorations. It underscores the enduring power of simplicity in unveiling complex ideas and its continuous relevance across multiple disciplines. The journey from understanding a simple equation like 3 x 2 to grasping its wider implications represents a fundamental step in developing a robust mathematical understanding. The simplicity of the equation belies its significance, demonstrating how even the most basic mathematical principles can contribute significantly to our comprehension of the world around us.
Latest Posts
Latest Posts
-
Lb Ft2 To Kn M2
Sep 09, 2025
-
In Regards Vs With Regards
Sep 09, 2025
-
7 1 7 Identify Types Of Vulnerabilities
Sep 09, 2025
-
Which Statement Describes The Trachea
Sep 09, 2025
-
Replication Transcription Translation Thinking Questions
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.