Solve 5 2x 25 4
khabri
Sep 10, 2025 · 5 min read
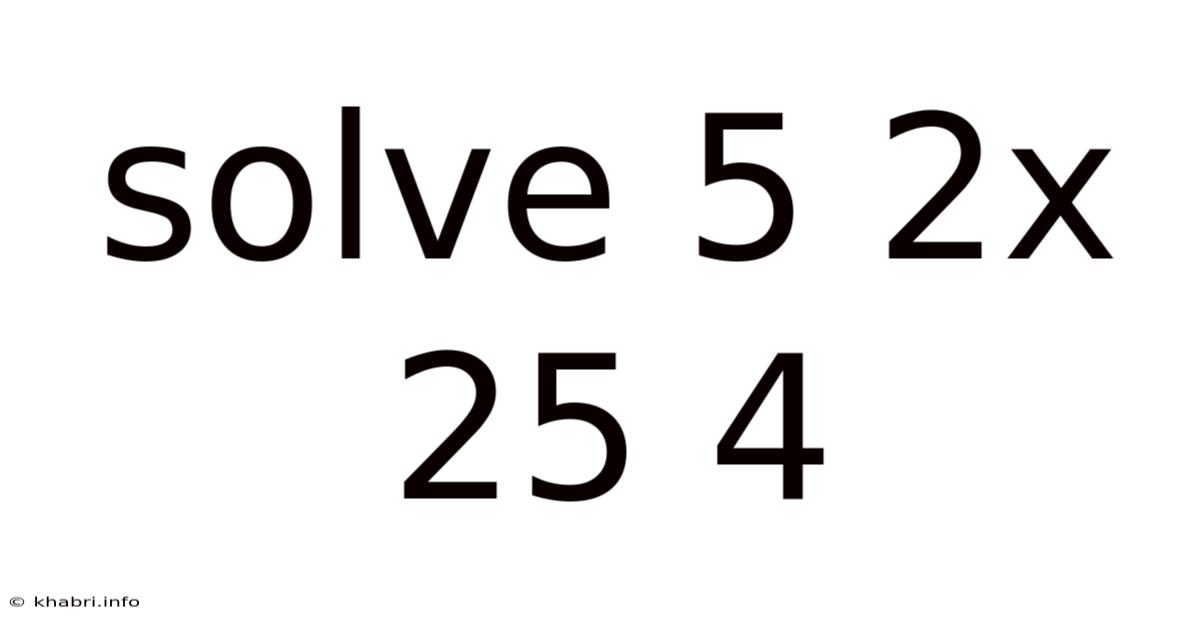
Table of Contents
Decoding the Mathematical Puzzle: Solve 5 + 2 x 25 + 4
This article delves into the seemingly simple yet often misunderstood mathematical puzzle: "Solve 5 + 2 x 25 + 4." Understanding the solution requires a grasp of the order of operations, also known as PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This seemingly straightforward equation highlights the importance of following a precise sequence to arrive at the correct answer. We'll not only solve the equation but also explore the underlying mathematical principles and address common misconceptions.
Understanding the Order of Operations (PEMDAS/BODMAS)
The foundation of solving this equation, and any equation involving multiple operations, lies in the order of operations. This standardized set of rules ensures that everyone arrives at the same solution. Both PEMDAS and BODMAS represent the same order:
- Parentheses/Brackets: Calculations within parentheses or brackets are always performed first.
- Exponents/Orders: Exponents (powers) and roots are evaluated next.
- Multiplication and Division: These operations are performed from left to right. Neither takes precedence over the other.
- Addition and Subtraction: Similar to multiplication and division, these are performed from left to right.
Step-by-Step Solution: 5 + 2 x 25 + 4
Now, let's apply the order of operations to solve our puzzle:
-
Multiplication First: The equation contains multiplication (2 x 25). Following PEMDAS/BODMAS, we perform this calculation before any addition:
2 x 25 = 50
-
Rewrite the Equation: Substitute the result back into the original equation:
5 + 50 + 4
-
Addition: Now, perform the addition from left to right:
5 + 50 = 55 55 + 4 = 59
Therefore, the solution to the equation 5 + 2 x 25 + 4 is 59.
Common Mistakes and Misconceptions
Many people make mistakes when solving this type of equation. The most common error stems from performing the operations from left to right without considering the order of operations. This leads to an incorrect answer. For example, an incorrect approach might be:
5 + 2 = 7 7 x 25 = 175 175 + 4 = 179
This method yields 179, which is incorrect. It is crucial to remember that multiplication and division always take precedence over addition and subtraction.
Another potential source of confusion arises from ambiguous notation or poorly written equations. In more complex equations, using parentheses to clarify the order of operations is vital to prevent mistakes.
Expanding the Understanding: More Complex Equations
The principles demonstrated in solving 5 + 2 x 25 + 4 can be applied to more complex equations. Let's consider a slightly more challenging example:
(10 + 5) x 2 – 3 x 4 + 12 ÷ 2
Following PEMDAS/BODMAS:
-
Parentheses/Brackets: First, we solve the expression inside the parentheses:
10 + 5 = 15
-
Rewrite the Equation: Replace the parenthetical expression with its result:
15 x 2 – 3 x 4 + 12 ÷ 2
-
Multiplication and Division (from left to right):
15 x 2 = 30 3 x 4 = 12 12 ÷ 2 = 6
-
Rewrite the Equation: Substitute the results of multiplication and division:
30 – 12 + 6
-
Addition and Subtraction (from left to right):
30 – 12 = 18 18 + 6 = 24
Therefore, the solution to (10 + 5) x 2 – 3 x 4 + 12 ÷ 2 is 24.
The Importance of Precision in Mathematics
The seemingly simple equation 5 + 2 x 25 + 4 serves as a powerful illustration of the importance of precision in mathematics. A slight deviation from the order of operations can lead to drastically different, and incorrect, results. Mastering the order of operations is fundamental for success in mathematics, forming a crucial building block for more advanced concepts and problem-solving.
Addressing Common Questions (FAQ)
Q: What happens if I use a calculator?
A: Most standard calculators are programmed to follow the order of operations (PEMDAS/BODMAS). However, some basic calculators might not, especially older models. It's always best to understand the underlying principles to ensure accuracy, regardless of the tool being used. Higher-end scientific calculators are designed to handle complex equations with appropriate parentheses and operational hierarchy.
Q: Why is the order of operations important?
A: The order of operations ensures consistency and unambiguous results. Without a standardized approach, different individuals could interpret the same mathematical statement differently, leading to conflicting answers. It's essential for clarity and collaboration in mathematics and scientific fields.
Q: Are there any exceptions to PEMDAS/BODMAS?
A: In general, PEMDAS/BODMAS is universally accepted. However, context and specific notations can sometimes modify the interpretation. For instance, the use of explicit grouping symbols (parentheses, brackets, braces) always takes precedence. Additionally, certain advanced mathematical contexts may introduce alternative notations or conventions, but these are usually clearly defined.
Q: How can I improve my understanding of the order of operations?
A: Practice is key! Work through a variety of equations of increasing complexity, ensuring you understand each step and the reason behind the order of operations. You can also find numerous online resources, including interactive exercises and tutorials, to further solidify your understanding.
Conclusion: Mastering the Fundamentals
Solving the equation 5 + 2 x 25 + 4, and similar equations, is more than just calculating a numerical result. It's about understanding and applying fundamental mathematical principles. The order of operations (PEMDAS/BODMAS) is a cornerstone of mathematical literacy. Mastering this concept opens doors to tackling more complex mathematical challenges and builds a solid foundation for future learning in algebra, calculus, and beyond. The consistent application of these rules ensures accurate results and promotes clear communication within the mathematical community. Always remember to prioritize multiplication and division before addition and subtraction!
Latest Posts
Latest Posts
-
Use Communism In A Sentence
Sep 10, 2025
-
Is Glycogen Phosphorylase A Kinase
Sep 10, 2025
-
Introductory Chemistry Tro 6th Edition
Sep 10, 2025
-
A Liquid Boils When Its
Sep 10, 2025
-
Label The Following Endocytosis Exocytosis Image
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Solve 5 2x 25 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.