Ln N 1 Ln N
khabri
Sep 15, 2025 · 6 min read
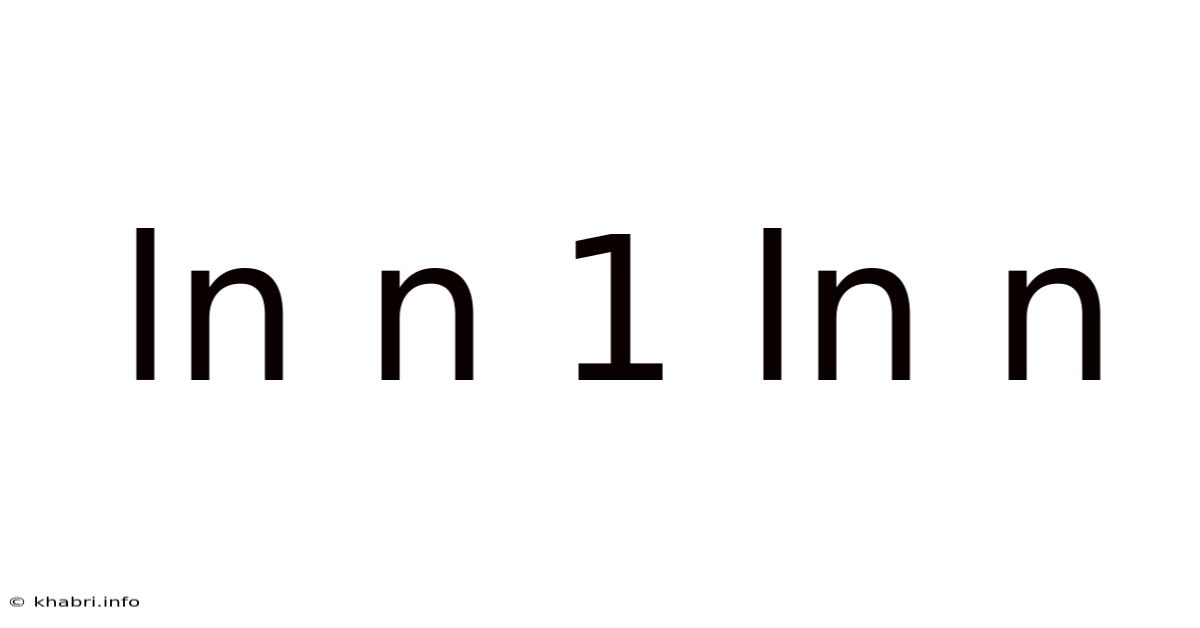
Table of Contents
Understanding the Behavior of ln(n) / (1 + ln(n))
This article delves into the mathematical analysis of the function ln(n) / (1 + ln(n)), exploring its behavior as 'n' approaches infinity, its limits, and its practical implications. We'll examine this seemingly simple function through a lens of calculus and limit theory, providing a comprehensive understanding suitable for students and enthusiasts alike. This exploration will cover its properties, derivative analysis, and asymptotic behavior, making it a valuable resource for anyone studying calculus, analysis, or related fields.
Introduction:
The function f(n) = ln(n) / (1 + ln(n)), where ln(n) represents the natural logarithm of n (log base e), is an interesting case study in asymptotic analysis. Understanding its behavior as n grows arbitrarily large is crucial in various applications, including algorithm analysis and the study of infinite series. At first glance, it might seem straightforward, but a deeper investigation reveals subtle nuances and important mathematical concepts. This analysis will provide a solid grounding in understanding how to analyze the behavior of such functions.
Understanding the Natural Logarithm (ln(n))
Before diving into the intricacies of our main function, let's refresh our understanding of the natural logarithm. The natural logarithm, denoted as ln(x) or logₑ(x), is the inverse function of the exponential function eˣ. In simpler terms, if eˣ = y, then ln(y) = x. The natural logarithm is defined only for positive values of x (x > 0). Its derivative is simply 1/x, a property that plays a significant role in our analysis. Crucially, ln(n) grows slowly as n increases, but it still tends to infinity as n approaches infinity. This slow growth is a key characteristic that impacts the behavior of our target function.
Analyzing the Function ln(n) / (1 + ln(n))
Let's now analyze the function f(n) = ln(n) / (1 + ln(n)). The function is defined for n > 0, since the natural logarithm is only defined for positive numbers. The denominator (1 + ln(n)) ensures that the function remains defined even when ln(n) approaches -1 (which it will never reach for positive n). The behavior of the function is most interesting as n approaches infinity.
Limit as n approaches Infinity
To understand the long-term behavior of f(n), we need to evaluate the limit as n approaches infinity:
lim (n→∞) [ln(n) / (1 + ln(n))]
This limit is an indeterminate form of type ∞/∞. We can use L'Hôpital's rule to evaluate it. L'Hôpital's rule states that if the limit of a function is in the indeterminate form 0/0 or ∞/∞, then the limit of the ratio of the derivatives is equal to the limit of the original ratio, provided the limit of the derivatives exists.
Applying L'Hôpital's rule:
We take the derivative of the numerator and the denominator separately with respect to n:
d(ln(n))/dn = 1/n d(1 + ln(n))/dn = 1/n
Therefore, the limit becomes:
lim (n→∞) [(1/n) / (1/n)] = lim (n→∞) 1 = 1
This result tells us that as n becomes infinitely large, the function f(n) approaches 1. This is a significant finding, indicating that the function's growth rate is asymptotically limited. It doesn't grow without bound; it approaches a finite value.
Derivative Analysis
Analyzing the derivative of f(n) provides further insight into its behavior. Let's find the derivative of f(n) using the quotient rule:
f'(n) = [ (1 + ln(n))(1/n) - ln(n)(1/n) ] / (1 + ln(n))² = [ 1/n + ln(n)/n - ln(n)/n ] / (1 + ln(n))² = 1 / [n(1 + ln(n))²]
Since n > 0 and (1 + ln(n))² > 0 for n > 1/e, f'(n) is always positive for sufficiently large n. This confirms that the function is monotonically increasing for sufficiently large n. However, the rate of increase slows down as n increases, consistent with the limit converging to 1.
Asymptotic Behavior and Big O Notation
In computer science and algorithm analysis, asymptotic behavior is crucial. We use Big O notation to describe the growth rate of functions. The Big O notation simplifies the analysis by focusing only on the dominant terms as the input size approaches infinity.
In our case, as n approaches infinity, f(n) approaches 1. Therefore, we can say that f(n) is O(1). This means that the function's growth is bounded by a constant, regardless of how large n becomes. This has significant implications for the efficiency of algorithms where this function might appear in complexity analysis. An O(1) algorithm is considered highly efficient.
Practical Implications and Applications
While this function might seem abstract, it has practical relevance in various fields:
-
Algorithm Analysis: If the runtime complexity of an algorithm involves this function, knowing its asymptotic behavior (O(1)) provides valuable insights into the algorithm's efficiency. It suggests that the algorithm's runtime doesn't increase significantly with the input size beyond a certain point.
-
Probability and Statistics: Functions of this nature can arise in probabilistic models and statistical analysis, where understanding their limiting behavior is crucial for interpreting results and drawing conclusions.
-
Numerical Analysis: In numerical methods, understanding the behavior of such functions is essential for assessing the convergence of iterative procedures and ensuring the accuracy of approximations.
-
Mathematical Modeling: The function could appear in the solutions to differential equations or in other mathematical models that describe real-world phenomena, allowing for analysis of the long-term behavior of the modeled system.
Frequently Asked Questions (FAQ)
-
Q: What happens when n is close to 0? A: The function is undefined for n ≤ 0 because the natural logarithm is not defined for non-positive numbers. As n approaches 0 from the right (n → 0+), ln(n) approaches negative infinity, and the function approaches 0.
-
Q: Is the function always increasing? A: While the derivative is positive for large n, indicating increasing behavior, there might be a region for small n where the function is not strictly increasing. A thorough analysis would be needed to determine the exact intervals of monotonicity.
-
Q: Can this function be expressed in a simpler form? A: While there isn't a significantly simpler algebraic representation, understanding its asymptotic behavior (approaching 1 as n → ∞) provides a practical simplification for many applications.
-
Q: What are the implications of the limit being 1? A: The limit being 1 signifies that the numerator and denominator grow at the same rate as n approaches infinity. The function essentially stabilizes around the value of 1, which is highly valuable for applications needing predictable long-term behavior.
Conclusion:
The function ln(n) / (1 + ln(n)) offers a compelling example of how to analyze the behavior of seemingly complex functions using tools from calculus and limit theory. Its asymptotic behavior (approaching 1 as n → ∞ and being O(1)) is crucial for various applications, particularly in algorithm analysis and mathematical modeling. By understanding its properties, derivative, and limiting behavior, we gain valuable insights into its practical implications and its role in various fields of study. This analysis highlights the importance of understanding the subtle nuances of mathematical functions and the power of analytical tools in unraveling their properties. The seemingly simple expression holds significant mathematical richness, underscoring the depth and importance of even seemingly elementary functions in advanced mathematical concepts.
Latest Posts
Latest Posts
-
Looking Out Looking In Book
Sep 15, 2025
-
Lewis Dot Structure For Bcl3
Sep 15, 2025
-
In Three Hours Company Abc
Sep 15, 2025
-
Inherent Rate Of Av Node
Sep 15, 2025
-
Rn Alterations In Hematologic Function
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Ln N 1 Ln N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.