Ln Infinity - Ln Infinity
khabri
Sep 11, 2025 · 5 min read
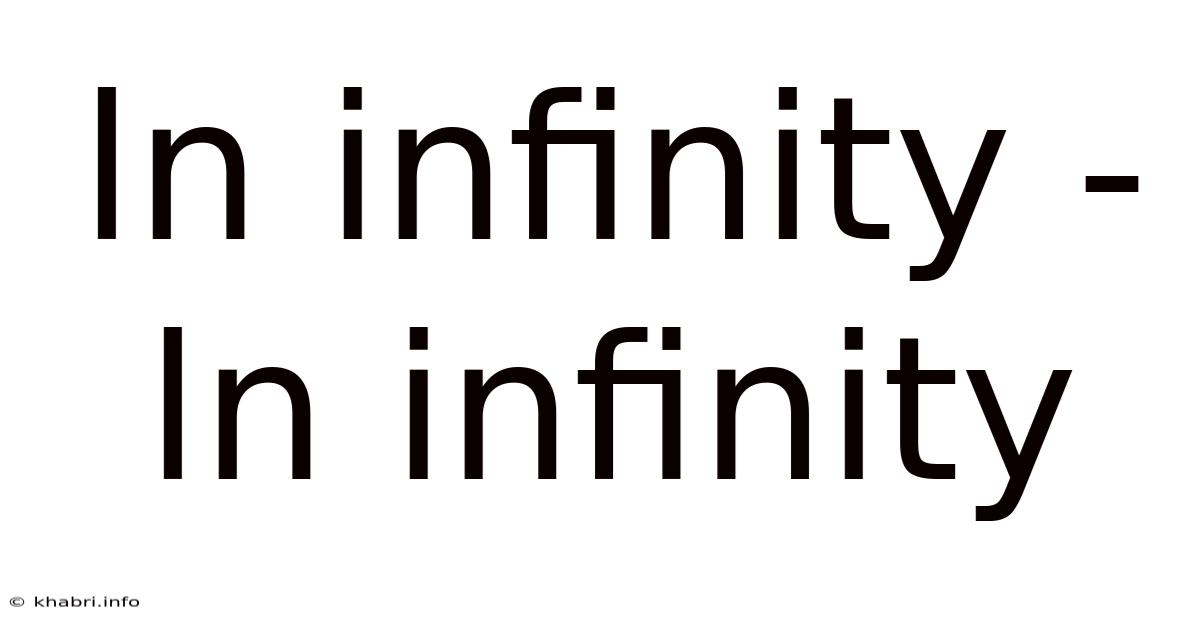
Table of Contents
Exploring the Indeterminate Form: ln(∞) - ln(∞)
The expression ln(∞) - ln(∞) represents an indeterminate form in calculus. This means that simply substituting infinity directly doesn't yield a meaningful result; the outcome depends entirely on the specific functions generating these infinite logarithms. Understanding how to resolve this indeterminate form is crucial for evaluating limits and solving various mathematical problems involving logarithmic functions and asymptotic behavior. This article delves into the intricacies of this indeterminate form, providing a comprehensive explanation with examples and demonstrating various approaches to evaluating such expressions.
Introduction to Indeterminate Forms
In calculus, indeterminate forms arise when evaluating limits where direct substitution leads to expressions like 0/0, ∞/∞, 0 × ∞, ∞ - ∞, 0⁰, 1⁰, and ∞⁰. These forms don't provide definitive answers without further investigation. The expression ln(∞) - ln(∞) falls into the ∞ - ∞ category, highlighting the need for careful analysis. The key to resolving such indeterminate forms lies in manipulating the expression algebraically or using L'Hôpital's rule to arrive at a determinate form that can be evaluated.
Understanding ln(∞)
The notation ln(∞) represents the limit of the natural logarithm function as its argument approaches infinity. Formally, we write:
lim<sub>x→∞</sub> ln(x) = ∞
This means that as x grows without bound, ln(x) also increases without bound. However, the rate at which ln(x) increases is significantly slower than x itself. This slow growth is a crucial aspect when dealing with logarithmic functions in limit calculations.
Resolving ln(∞) - ln(∞): Techniques and Examples
The resolution of ln(∞) - ln(∞) heavily relies on the specific functions that generate these infinite logarithms. Let's examine some common scenarios and techniques:
1. Using Logarithmic Properties:
The most straightforward approach often involves utilizing the properties of logarithms. Recall that ln(a) - ln(b) = ln(a/b). Applying this property to ln(∞) - ln(∞), we get:
ln(∞) - ln(∞) = ln(∞/∞)
This transforms the ∞ - ∞ indeterminate form into the ∞/∞ indeterminate form, which can then be tackled using L'Hôpital's Rule (explained in the next section). However, simply writing ln(∞/∞) is not sufficient; we need the original functions to rewrite the expression correctly.
Example 1:
Consider the limit:
lim<sub>x→∞</sub> [ln(x² + 1) - ln(x)]
Here, we have an expression of the form ln(∞) - ln(∞). Applying the logarithmic property:
lim<sub>x→∞</sub> [ln(x² + 1) - ln(x)] = lim<sub>x→∞</sub> ln[(x² + 1)/x] = lim<sub>x→∞</sub> ln(x + 1/x)
As x approaches infinity, 1/x approaches 0. Therefore:
lim<sub>x→∞</sub> ln(x + 1/x) = lim<sub>x→∞</sub> ln(x) = ∞
Therefore, the limit evaluates to infinity.
Example 2:
Let's analyze a slightly more complex case:
lim<sub>x→∞</sub> [ln(e<sup>x</sup> + x) - ln(e<sup>x</sup>)]
Using the logarithmic property:
lim<sub>x→∞</sub> [ln(e<sup>x</sup> + x) - ln(e<sup>x</sup>)] = lim<sub>x→∞</sub> ln[(e<sup>x</sup> + x)/e<sup>x</sup>] = lim<sub>x→∞</sub> ln[1 + x/e<sup>x</sup>]
Since the exponential function grows much faster than any polynomial function, the limit of x/e<sup>x</sup> as x approaches infinity is 0. Therefore:
lim<sub>x→∞</sub> ln[1 + x/e<sup>x</sup>] = ln(1 + 0) = ln(1) = 0
In this instance, the limit evaluates to 0. These examples illustrate that the outcome of ln(∞) - ln(∞) is highly dependent on the specific functions involved.
2. L'Hôpital's Rule:
L'Hôpital's Rule is a powerful tool for evaluating limits involving indeterminate forms. If we have a limit of the form ∞/∞ or 0/0, then under certain conditions, we can take the derivative of the numerator and the denominator separately and evaluate the limit of the resulting expression. This process can be iterated if necessary.
However, to apply L'Hôpital's Rule to ln(∞) - ln(∞), we must first rewrite the expression in the form of a fraction using logarithmic properties, as demonstrated in the previous section. Only then can we differentiate the numerator and denominator.
Example 3 (Applying L'Hôpital's Rule):
Consider the limit:
lim<sub>x→∞</sub> [ln(x + 1) - ln(x)]
Using the logarithmic property:
lim<sub>x→∞</sub> ln[(x + 1)/x] = lim<sub>x→∞</sub> ln(1 + 1/x)
This is still an indeterminate form, but direct substitution gives us ln(1) = 0. However, let's proceed with a different approach to demonstrate L'Hopital's Rule for a similar function.
Let's slightly modify the function to have a more involved application of L'Hopital's rule:
lim<sub>x→∞</sub> [ln(x² + 1) - ln(x)] = lim<sub>x→∞</sub> ln[(x² + 1)/x] = lim<sub>x→∞</sub> ln(x + 1/x)
This limit is still of the form ln(∞), which is not an indeterminate form, directly resulting in ∞. A more illustrative example needing L'Hôpital's rule is needed.
Consider a more complex scenario where a different approach is needed:
lim<sub>x→∞</sub> [ln(x² + x) - ln(x²)] = lim<sub>x→∞</sub> ln[(x² + x)/x²] = lim<sub>x→∞</sub> ln(1 + 1/x)
This limit directly evaluates to ln(1) = 0. L'Hopital's Rule isn't directly applicable here because we don't have an indeterminate form after applying the logarithmic properties.
3. Taylor Series Expansion:
For some expressions involving ln(∞) - ln(∞), a Taylor series expansion can provide a useful alternative method. By approximating the functions within the logarithms using their Taylor series around a specific point, we can often simplify the expression and evaluate the limit.
Conclusion
The indeterminate form ln(∞) - ln(∞) highlights the importance of careful algebraic manipulation and understanding the behavior of logarithmic functions. There is no single solution; the approach depends entirely on the specific functions within the expression. Mastering the techniques outlined above—primarily using logarithmic properties and, where appropriate, L'Hôpital's Rule—is essential for effectively handling such situations in calculus and related fields. Always remember to simplify the expression using logarithmic rules before considering more advanced techniques like L'Hôpital's Rule or Taylor series expansion. The examples provided showcase the variety of outcomes possible, underscoring the need for careful consideration of each problem's unique characteristics. Practice with diverse examples is key to developing proficiency in handling this crucial indeterminate form.
Latest Posts
Latest Posts
-
Single Strand Binding Proteins Function
Sep 11, 2025
-
Does So3 2 Have Resonance
Sep 11, 2025
-
Combining Form For Urinary Bladder
Sep 11, 2025
-
Reading The World Michael Austin
Sep 11, 2025
-
Essentials Of Oceanography 8th Edition
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Ln Infinity - Ln Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.