Integrate X Ln X 2
khabri
Sep 16, 2025 · 5 min read
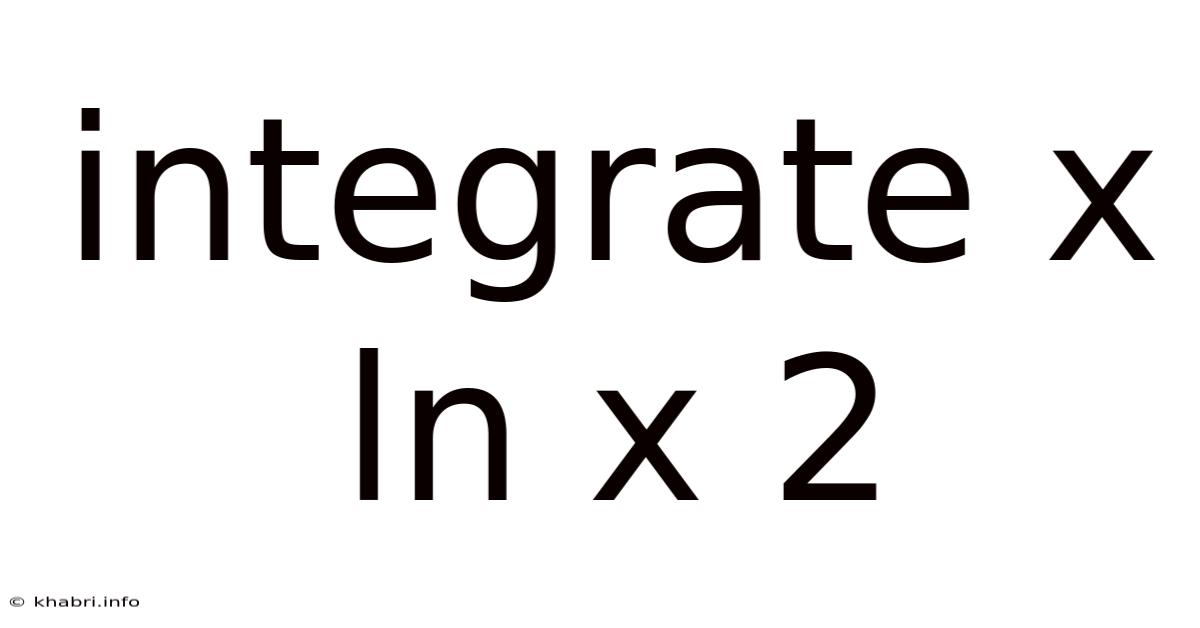
Table of Contents
Integrating x ln(x²) : A Comprehensive Guide
Integrating functions involving logarithmic and polynomial terms is a common task in calculus. This article provides a detailed explanation of how to integrate the function x ln(x²), exploring different approaches and offering insights into the underlying mathematical principles. We'll cover various integration techniques, delve into the scientific rationale behind each step, and address frequently asked questions to solidify your understanding. This comprehensive guide will equip you with the knowledge to tackle similar integration problems confidently.
Introduction: Understanding the Problem
The integral we aim to solve is ∫x ln(x²) dx. This seemingly simple integral requires a strategic approach due to the product of a polynomial function (x) and a logarithmic function (ln(x²)). Direct integration isn't feasible; we need to employ a technique called integration by parts. Before we delve into the solution, let's review the fundamental concepts.
Key Concepts:
- Integration by Parts: This technique is crucial for integrating products of functions. It's based on the product rule of differentiation, expressed as: ∫u dv = uv - ∫v du, where 'u' and 'v' are functions of x.
- Logarithmic Properties: Understanding logarithmic properties is essential for simplifying the integrand. Specifically, the property ln(aᵇ) = b ln(a) will be vital in our solution.
- Power Rule of Integration: We'll also use the power rule, which states: ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where 'n' is a constant and 'C' is the constant of integration.
Step-by-Step Solution using Integration by Parts
Let's solve ∫x ln(x²) dx using integration by parts.
1. Simplify the Integrand:
First, we simplify the integrand using the logarithmic property ln(aᵇ) = b ln(a):
ln(x²) = 2 ln(x)
Therefore, our integral becomes:
∫x (2 ln(x)) dx = 2 ∫x ln(x) dx
Now we have a simpler integral to work with: 2 ∫x ln(x) dx
2. Apply Integration by Parts:
We choose our 'u' and 'dv' as follows:
- u = ln(x) => du = (1/x) dx
- dv = x dx => v = (x²/2)
Now, we apply the integration by parts formula:
∫u dv = uv - ∫v du
Substituting our values:
2 ∫x ln(x) dx = 2 [ (ln(x))(x²/2) - ∫(x²/2)(1/x) dx ]
3. Simplify and Integrate:
Simplify the expression inside the brackets:
2 [ (x² ln(x))/2 - ∫(x/2) dx ]
Now integrate the remaining term:
2 [ (x² ln(x))/2 - (x²/4) ]
4. Final Solution:
Distribute the '2' and add the constant of integration 'C':
x² ln(x) - x²/2 + C
Therefore, the final solution to the integral ∫x ln(x²) dx is x² ln(x) - x²/2 + C.
Alternative Approach: Substitution Method
While integration by parts is the most straightforward approach, we can also explore an alternative method using substitution. However, this method is slightly less intuitive for this specific problem.
1. Substitute u = ln(x²):
This implies du = (2/x) dx. We can rewrite the integral as:
∫x ln(x²) dx = ∫x * u * (x/2) du = (1/2) ∫x²u du
This substitution doesn't directly simplify the integral to a readily solvable form. The presence of x² makes it difficult to express the integral entirely in terms of 'u'.
2. Re-express in terms of x:
To overcome this, we could express x² in terms of 'u' using the relationship u = ln(x²), which implies eᵘ = x². However, this leads to a more complex integral and isn't as efficient as the integration by parts method in this case.
Therefore, for this particular problem, integration by parts is the more effective and efficient approach.
Scientific Rationale and Explanation
The success of the integration by parts method hinges on the careful selection of 'u' and 'dv'. The choice of u = ln(x) is strategic because its derivative, du = (1/x) dx, simplifies the integral considerably. Choosing dv = x dx results in a readily integrable function v = (x²/2). This combination streamlines the process, transforming a complex integral into a manageable one. The underlying principle is reducing the complexity of the integral by strategically applying the product rule in reverse.
Frequently Asked Questions (FAQ)
Q1: What if the exponent of x was different?
A1: If the integral was, for example, ∫x² ln(x²) dx, we would still use integration by parts, but the choice of 'u' and 'dv' might change. The process remains similar, but the resulting integral will be different.
Q2: What is the constant of integration 'C', and why is it important?
A2: The constant of integration 'C' represents an arbitrary constant that can take any real value. It's crucial because the derivative of a constant is zero. Therefore, when we differentiate the result of our integration, the 'C' disappears, reflecting that multiple functions can have the same derivative.
Q3: Can I use a calculator or software to verify my answer?
A3: Yes, many computer algebra systems (CAS) and online calculators can perform symbolic integration. You can use these tools to verify your answer, but it's important to understand the underlying mathematical steps to fully grasp the concept.
Q4: Are there any other techniques to solve this integral?
A4: While integration by parts is the most direct and effective method, other more complex techniques, potentially involving series expansions, could be used. However, these methods are significantly less practical and efficient for this specific problem.
Conclusion: Mastering Integration Techniques
This comprehensive guide has demonstrated the effective use of integration by parts to solve the integral ∫x ln(x²) dx. We've explored the underlying mathematical principles, addressed potential alternative approaches, and answered frequently asked questions to enhance your understanding. Mastering integration techniques, particularly integration by parts, is crucial for solving various problems in calculus and its applications in science and engineering. Remember to carefully choose your 'u' and 'dv' to simplify the integration process and always remember to include the constant of integration 'C' in your final answer. The ability to solve integrals like this one demonstrates a solid understanding of fundamental calculus concepts. Consistent practice and a clear understanding of the underlying theory will enable you to tackle more complex integration problems with confidence.
Latest Posts
Latest Posts
-
5 1 4 Access For Dna Class
Sep 16, 2025
-
Norkin Measurement Of Joint Motion
Sep 16, 2025
-
Most Spells Of Unemployment Are
Sep 16, 2025
-
Kn M3 To Lb Ft3
Sep 16, 2025
-
Which Combining Form Means Bone
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integrate X Ln X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.