Integral X 2 Sin 2x
khabri
Sep 13, 2025 · 5 min read
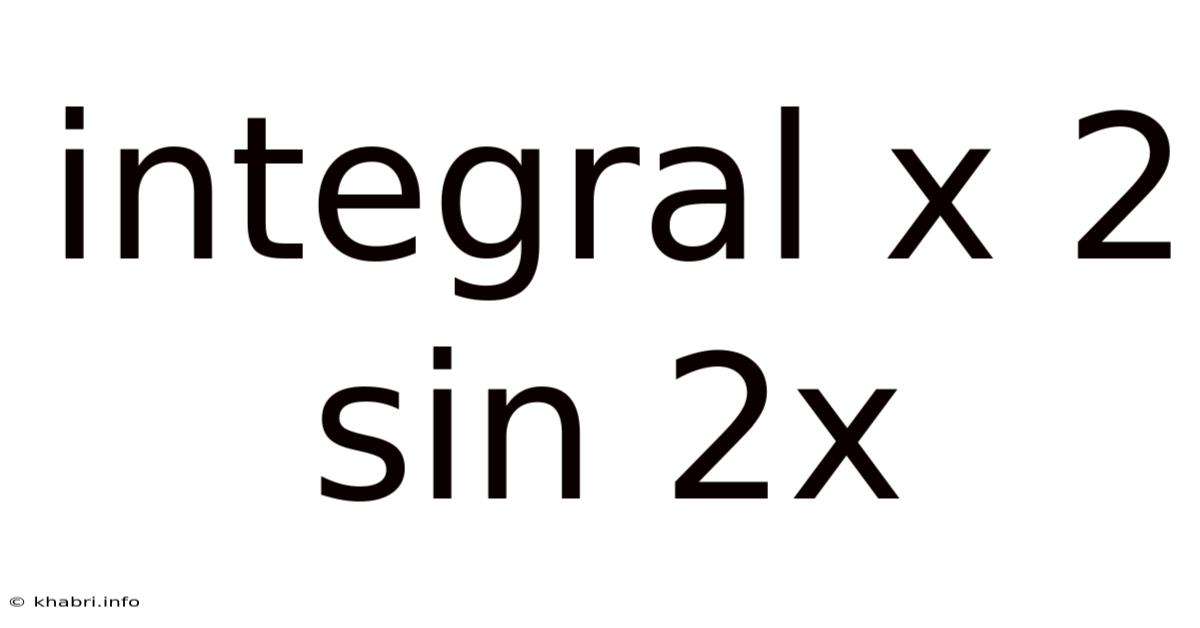
Table of Contents
Solving the Integral of 2sin(2x): A Comprehensive Guide
This article provides a comprehensive guide on how to solve the definite and indefinite integral of 2sin(2x), exploring various methods and delving into the underlying mathematical principles. Understanding this integral is crucial for many applications in calculus, physics, and engineering. We'll cover the solution process step-by-step, making it accessible for students of all levels, from beginners grappling with basic integration techniques to those seeking a deeper understanding of integration by substitution. We will also address common questions and potential pitfalls.
1. Introduction: Understanding the Problem
The problem before us is to evaluate the integral of 2sin(2x) with respect to x. This involves finding a function whose derivative is 2sin(2x). This seemingly simple problem introduces fundamental concepts of integration, particularly the chain rule in reverse and the use of substitution. The integral can be expressed in two forms: the indefinite integral, represented as ∫2sin(2x)dx, and the definite integral, represented as ∫<sub>a</sub><sup>b</sup>2sin(2x)dx, where 'a' and 'b' are the limits of integration. Both forms are crucial to master for a complete understanding of integration techniques. We'll tackle both, ensuring a thorough comprehension of the subject matter.
2. Solving the Indefinite Integral: ∫2sin(2x)dx
The key to solving this integral lies in the application of integration by substitution. This technique simplifies complex integrals by replacing a part of the integrand with a new variable, making the integral easier to manage.
Steps:
-
Substitution: Let's substitute u = 2x. This simplifies the integrand.
-
Differentiate: Now we find the differential of u with respect to x: du/dx = 2. Rearranging this gives dx = du/2.
-
Substitute into the Integral: Replace 2x with u and dx with du/2 in the original integral:
∫2sin(2x)dx = ∫2sin(u)(du/2)
-
Simplify: The 2's cancel out, leaving a much simpler integral:
∫sin(u)du
-
Integrate: The integral of sin(u) with respect to u is -cos(u) + C, where C is the constant of integration (a crucial element in indefinite integrals).
-
Back-Substitute: Replace u with 2x to express the result in terms of the original variable x:
-cos(2x) + C
Therefore, the indefinite integral of 2sin(2x) is -cos(2x) + C.
3. Solving the Definite Integral: ∫<sub>a</sub><sup>b</sup>2sin(2x)dx
Solving the definite integral involves the same substitution method but adds an extra step of evaluating the result at the limits of integration. Let's assume our limits are 'a' and 'b'.
Steps:
-
Follow Steps 1-5 from the indefinite integral solution. This gives us -cos(u) + C.
-
Evaluate at Limits: Substitute the limits of integration 'a' and 'b' back into the expression, replacing u with 2x:
[-cos(2b) + C] - [-cos(2a) + C]
-
Simplify: Notice that the constant of integration, C, cancels out. This is a characteristic of definite integrals; the constant of integration always cancels when evaluating between limits. This leaves us with:
-cos(2b) + cos(2a)
Therefore, the definite integral of 2sin(2x) from a to b is -cos(2b) + cos(2a) or equivalently cos(2a) - cos(2b).
4. Explanation Using the Chain Rule (in reverse)
The substitution method is essentially applying the chain rule in reverse. Recall the chain rule for differentiation: d/dx[f(g(x))] = f'(g(x)) * g'(x). When we integrate, we're essentially undoing this process.
Consider the derivative of -cos(2x):
d/dx[-cos(2x)] = sin(2x) * 2 (using the chain rule)
This shows that -cos(2x) is an antiderivative of 2sin(2x). The constant of integration accounts for all other possible antiderivatives. This provides a direct link between differentiation and integration, reinforcing the fundamental theorem of calculus.
5. Practical Applications
The integral of 2sin(2x) has numerous applications across various fields:
-
Physics: Describing oscillatory motion (like a simple harmonic oscillator), calculating work done by a varying force, analyzing wave phenomena.
-
Engineering: Modeling vibrations in mechanical systems, analyzing alternating current circuits, signal processing.
-
Calculus: Demonstrating integration techniques, understanding the relationship between differentiation and integration.
6. Common Mistakes and Pitfalls
-
Forgetting the Constant of Integration (C): This is crucial for indefinite integrals. Omitting it is a common mistake.
-
Incorrect Substitution: Ensure the substitution is correctly performed and the differentials are handled accurately.
-
Errors in Simplification: Pay attention to algebraic manipulations to avoid mistakes.
-
Incorrect Evaluation of Definite Integrals: Carefully substitute the limits of integration and handle the subtraction correctly.
7. Frequently Asked Questions (FAQ)
-
Q: What if the coefficient of sin(2x) was different from 2?
A: The process remains the same. For example, if the integral was ∫k*sin(2x)dx, where k is a constant, the solution would be -(k/2)cos(2x) + C. The constant simply carries through the integration.
-
Q: Can I use other integration techniques to solve this?
A: While substitution is the most straightforward and efficient approach, you could potentially use integration by parts, although this would be more complicated and less efficient for this particular problem.
-
Q: What if the argument of the sine function was different? For example, ∫2sin(3x)dx?
A: The approach is similar. Substitute u = 3x, du = 3dx, and proceed as before. The solution will be -(2/3)cos(3x) + C. The coefficient of x inside the sine function affects the constant factor in the final result.
8. Conclusion
Solving the integral of 2sin(2x) is a fundamental exercise that reinforces essential calculus concepts. The method of substitution, explained in detail above, provides a clear and efficient path to both the indefinite and definite integrals. Understanding this example solidifies the connection between differentiation and integration and showcases the power and versatility of substitution as a crucial integration technique. Remember to pay attention to detail, particularly in handling the substitution and limits of integration, to avoid common mistakes. Through practice and a firm grasp of the underlying principles, you can confidently tackle more complex integrals and applications in various fields. Mastering this seemingly simple integral lays a strong foundation for further exploration in the fascinating world of calculus.
Latest Posts
Latest Posts
-
Concept Map Of Dna Replication
Sep 13, 2025
-
Experts Categorize Problems Based On
Sep 13, 2025
-
Oxygen Crosses A Plasma Membrane
Sep 13, 2025
-
In A Solution The Solvent
Sep 13, 2025
-
Conjugate Base Of Hpo4 2
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Integral X 2 Sin 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.