Integral 2x 3 2 Dx
khabri
Sep 11, 2025 · 6 min read
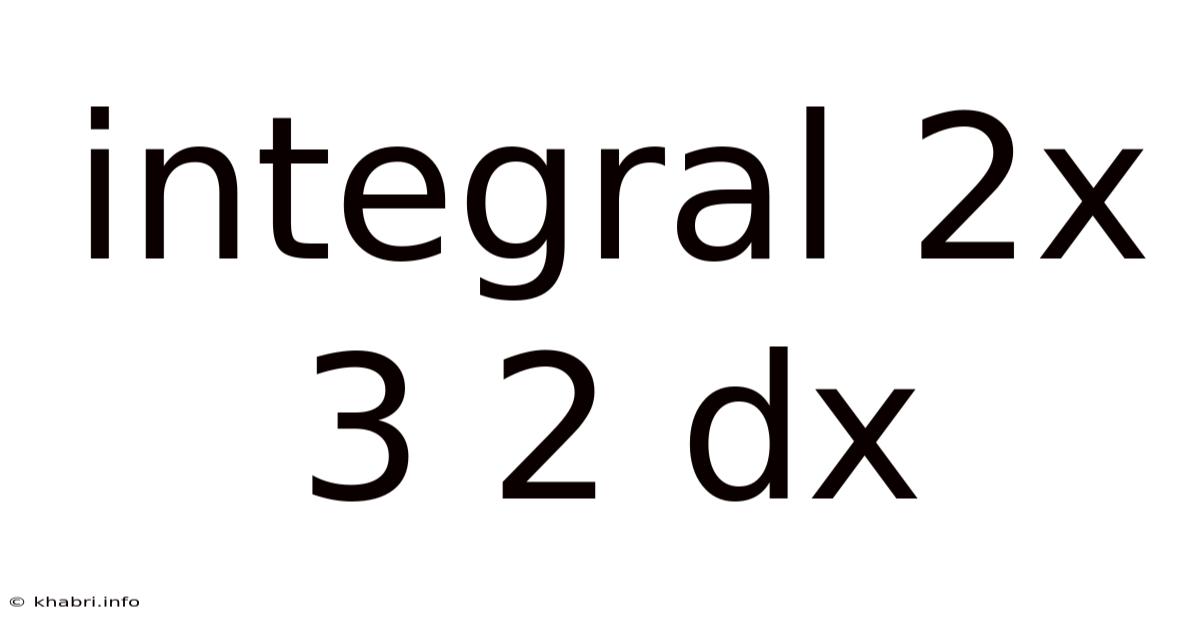
Table of Contents
Definite and Indefinite Integrals: A Deep Dive into ∫2x³ + 2 dx
This article provides a comprehensive guide to solving the integral ∫(2x³ + 2) dx, covering both definite and indefinite integrals. We'll explore the fundamental concepts of integration, the power rule, and how to apply them to solve this specific problem, along with tackling potential related questions. Understanding this seemingly simple integral lays the groundwork for tackling more complex integration problems in calculus.
Understanding Integrals: The Foundation
Before diving into the solution, let's establish a firm understanding of what an integral represents. In calculus, integration is the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the area under the curve of a function.
There are two main types of integrals:
-
Indefinite Integrals: These represent a family of functions whose derivative is the integrand (the function being integrated). They are denoted by ∫f(x) dx and always include a constant of integration, "+C," because the derivative of a constant is zero.
-
Definite Integrals: These represent the numerical value of the area under the curve of a function between two specified limits of integration. They are denoted by ∫<sub>a</sub><sup>b</sup>f(x) dx, where 'a' and 'b' are the lower and upper limits, respectively.
Solving the Indefinite Integral ∫(2x³ + 2) dx
Our problem is to solve ∫(2x³ + 2) dx. This is an indefinite integral, meaning we're looking for a function whose derivative is 2x³ + 2. We'll use the power rule of integration to solve this.
The power rule states that the integral of x<sup>n</sup> dx is (x<sup>n+1</sup>)/(n+1) + C, where n ≠ -1 and C is the constant of integration.
Let's break down the integral:
∫(2x³ + 2) dx = ∫2x³ dx + ∫2 dx
Applying the power rule to each term:
-
∫2x³ dx: Here, n = 3. Using the power rule, we get (2x<sup>3+1</sup>)/(3+1) = (2x⁴)/4 = x⁴/2.
-
∫2 dx: Here, we can rewrite 2 as 2x⁰. Using the power rule, we get (2x⁰⁺¹)/(0+1) = 2x.
Combining these results, we get:
∫(2x³ + 2) dx = x⁴/2 + 2x + C
Therefore, the indefinite integral of 2x³ + 2 is x⁴/2 + 2x + C, where C is the constant of integration. This "C" represents an infinite number of possible functions that could have 2x³ + 2 as their derivative, differing only by a constant vertical shift.
Solving Definite Integrals: Adding Limits
Now, let's consider what happens when we add limits of integration. A definite integral gives a numerical value representing the area under the curve between two points. Let's say we want to find the definite integral:
∫<sub>1</sub><sup>3</sup>(2x³ + 2) dx
We first find the indefinite integral, which we already determined to be x⁴/2 + 2x + C. The crucial step is evaluating this indefinite integral at the upper and lower limits and then subtracting the results. Notice that the constant of integration "+C" cancels out when we do this subtraction.
-
Evaluate at the upper limit (x = 3): (3⁴/2) + 2(3) = 81/2 + 6 = 93/2
-
Evaluate at the lower limit (x = 1): (1⁴/2) + 2(1) = 1/2 + 2 = 5/2
-
Subtract the lower limit result from the upper limit result: (93/2) - (5/2) = 88/2 = 44
Therefore, the definite integral ∫<sub>1</sub><sup>3</sup>(2x³ + 2) dx = 44. This means that the area under the curve y = 2x³ + 2 between x = 1 and x = 3 is 44 square units.
The Geometric Interpretation and Riemann Sums
It’s important to visualize what the integral represents geometrically. The definite integral calculates the signed area between the curve and the x-axis. Areas above the x-axis are positive, and areas below are negative.
The concept of the integral can be understood through Riemann sums. A Riemann sum approximates the area under a curve by dividing the area into a series of rectangles. As the width of these rectangles approaches zero (the number of rectangles approaches infinity), the Riemann sum converges to the exact value of the definite integral. This provides a fundamental link between geometry and calculus.
Further Applications and Extensions
The integral ∫(2x³ + 2) dx, while seemingly simple, forms a building block for more complex problems. Understanding this integral is crucial for:
-
Calculating areas and volumes: Integration is fundamental in calculating areas of irregular shapes and volumes of solids of revolution.
-
Solving differential equations: Many physical phenomena are modeled using differential equations, and integration is essential for finding their solutions.
-
Probability and statistics: Integrals are used extensively in probability theory to calculate probabilities and expected values.
-
Engineering and physics: From calculating work done by a force to determining the center of mass of an object, integration is ubiquitous in engineering and physics applications.
Frequently Asked Questions (FAQ)
Q1: What if the integrand contains other functions?
A1: The power rule is specifically for terms of the form x<sup>n</sup>. If the integrand contains other functions like trigonometric functions (sin x, cos x), exponential functions (e<sup>x</sup>), or logarithmic functions (ln x), you'll need to apply appropriate integration techniques such as substitution, integration by parts, or partial fraction decomposition.
Q2: Why is the constant of integration "+C" important in indefinite integrals?
A2: The constant of integration represents the family of functions that have the same derivative. Since the derivative of a constant is zero, adding any constant to the antiderivative will not change its derivative.
Q3: Can I use a calculator or software to solve integrals?
A3: Yes, many calculators and software packages (like Wolfram Alpha or symbolic math software) can solve integrals, but understanding the underlying principles remains crucial for applying integration effectively in various contexts. Tools are helpful for verification but shouldn't replace understanding the process.
Q4: What if the limits of integration are infinite?
A4: This involves improper integrals, requiring the use of limits. You would evaluate the integral using limits as the upper or lower limit approaches infinity. The integral might converge to a finite value, diverge to infinity, or oscillate.
Q5: How does integration relate to differentiation?
A5: Integration is the inverse operation of differentiation. If you differentiate the result of an indefinite integral (excluding the constant of integration), you obtain the original integrand. This forms the fundamental theorem of calculus.
Conclusion
This comprehensive guide has detailed the process of solving the integral ∫(2x³ + 2) dx, both indefinitely and with specified limits. We’ve covered the power rule, the significance of the constant of integration, the geometric interpretation of the integral, and addressed common questions. Remember that mastering integration is a journey that builds upon fundamental concepts and expands into more advanced techniques. The simple integral examined here provides a solid foundation for tackling more complex integrations in the future. Keep practicing, and you will develop a strong understanding of this essential tool in calculus and its applications.
Latest Posts
Latest Posts
-
Virtual Bacterial Id Lab Answers
Sep 11, 2025
-
Life Span Human Development 10th Edition
Sep 11, 2025
-
Electroplating With Copper Lab Answers
Sep 11, 2025
-
Label The Major Systemic Arteries
Sep 11, 2025
-
13 Out Of 17 Percentage
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Integral 2x 3 2 Dx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.