Graph Y 1 2f X
khabri
Sep 14, 2025 · 7 min read
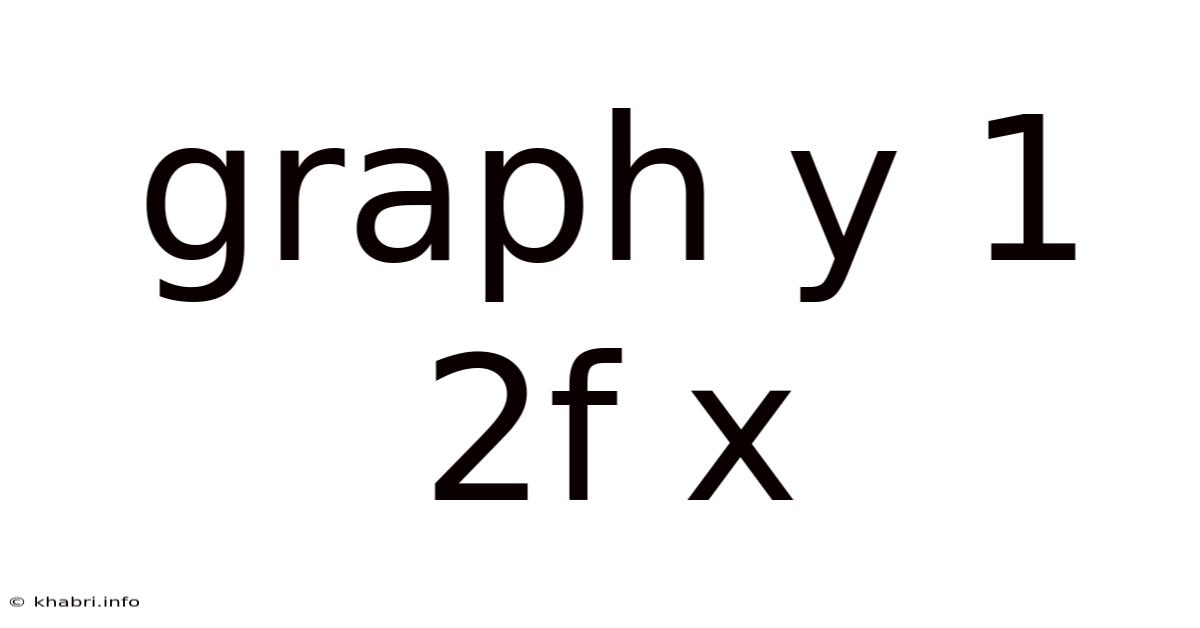
Table of Contents
Decoding the Graph of y = 1/2f(x): A Comprehensive Guide
Understanding transformations of functions is a cornerstone of algebra and calculus. This article delves deep into the graph of y = 1/2f(x), exploring its relationship to the parent function f(x), the transformations involved, and the implications for various mathematical concepts. We will break down the process step-by-step, providing a clear and comprehensive understanding for students of all levels. This guide will cover the key aspects of vertical scaling, identifying key features, and applying this knowledge to different types of functions.
Introduction: Understanding Function Transformations
Before we dive into the specifics of y = 1/2f(x), let's review the basics of function transformations. Transformations alter the graph of a function without changing its fundamental properties. Common transformations include:
- Vertical Shifts: Adding a constant to the function (e.g., f(x) + c) shifts the graph vertically upwards (if c > 0) or downwards (if c < 0).
- Horizontal Shifts: Adding a constant inside the function (e.g., f(x + c)) shifts the graph horizontally to the left (if c > 0) or to the right (if c < 0).
- Vertical Scaling: Multiplying the function by a constant (e.g., cf(x)) stretches or compresses the graph vertically. If |c| > 1, it's a stretch; if 0 < |c| < 1, it's a compression. If c is negative, there's also a reflection across the x-axis.
- Horizontal Scaling: Multiplying the input by a constant (e.g., f(cx)) stretches or compresses the graph horizontally. If |c| > 1, it's a compression; if 0 < |c| < 1, it's a stretch. If c is negative, there's also a reflection across the y-axis.
In the equation y = 1/2f(x), we are focusing on vertical scaling.
The Transformation: y = 1/2f(x)
The equation y = 1/2f(x) represents a vertical compression of the parent function f(x) by a factor of 1/2. This means that every y-coordinate of the original graph is multiplied by 1/2. The x-coordinates remain unchanged.
Let's break this down visually:
Imagine a point (a, b) on the graph of y = f(x). This means that f(a) = b. On the graph of y = 1/2f(x), the corresponding point will be (a, 1/2b). This transformation shrinks the vertical distance of every point from the x-axis to half its original value.
Key Observations:
- x-intercepts remain unchanged: Since the transformation only affects the y-coordinates, any point where the graph intersects the x-axis (i.e., where y = 0) will remain unchanged. The x-intercepts of f(x) and 1/2f(x) are identical.
- y-intercept is scaled: The y-intercept of f(x) is f(0). The y-intercept of 1/2f(x) will be (1/2)f(0).
- Relative extrema are scaled: If f(x) has a maximum or minimum value at a specific x-coordinate, the corresponding value in 1/2f(x) will be half as large. The x-coordinates of the extrema remain the same.
- Asymptotes are affected: If f(x) has horizontal or vertical asymptotes, these will be affected by the transformation. Horizontal asymptotes will be scaled vertically by a factor of 1/2. Vertical asymptotes will remain unchanged as they are defined by x-values where the function is undefined.
Step-by-Step Graphical Analysis
To effectively analyze the graph of y = 1/2f(x), follow these steps:
- Sketch the graph of f(x): Start by plotting the parent function. This forms the basis for understanding the transformation.
- Identify key points: Pinpoint important points on the graph of f(x), such as x-intercepts, y-intercepts, extrema (maxima and minima), and asymptotes.
- Apply the transformation: For each key point (a, b) on f(x), find the corresponding point (a, 1/2b) on the graph of y = 1/2f(x).
- Connect the transformed points: Smoothly connect the transformed points to create the graph of y = 1/2f(x). Maintain the overall shape and characteristics of the original function, but remember the vertical compression.
- Label key features: Clearly label the transformed key points, intercepts, extrema, and asymptotes on the graph of y = 1/2f(x).
Examples with Different Parent Functions
Let's illustrate the transformation with different types of parent functions:
Example 1: f(x) = x² (A Parabola)
The graph of f(x) = x² is a parabola opening upwards with its vertex at (0, 0). The graph of y = 1/2f(x) = 1/2x² is also a parabola opening upwards, but it's compressed vertically. The vertex remains at (0, 0), but other points are closer to the x-axis. For instance, the point (1, 1) on f(x) becomes (1, 1/2) on y = 1/2x².
Example 2: f(x) = sin(x) (A Trigonometric Function)
The graph of f(x) = sin(x) is a wave oscillating between -1 and 1. The graph of y = 1/2sin(x) is also a wave, but its amplitude is reduced to 1/2. It oscillates between -1/2 and 1/2. The period and the x-intercepts remain the same.
Example 3: f(x) = 1/x (A Hyperbolic Function)
The graph of f(x) = 1/x has two branches in quadrants I and III, with asymptotes at x = 0 and y = 0. The graph of y = 1/2(1/x) = 1/(2x) is also a hyperbolic function, but the branches are closer to the x-axis. The vertical asymptote remains at x = 0, but the horizontal asymptote remains at y = 0.
Mathematical Implications and Applications
Understanding the transformation y = 1/2f(x) has implications for various mathematical concepts:
- Calculus: Finding derivatives and integrals of transformed functions. The derivative of 1/2f(x) is (1/2)f'(x), and the integral involves a similar scaling factor.
- Differential Equations: Solving differential equations involving transformed functions.
- Modeling: Using transformed functions to model real-world phenomena where a scaling factor is involved. For example, scaling down the amplitude of a wave or reducing the magnitude of a force.
Frequently Asked Questions (FAQ)
Q1: What happens if the scaling factor is greater than 1?
A1: If the scaling factor is greater than 1 (e.g., y = 2f(x)), the graph is vertically stretched instead of compressed. Every y-coordinate is multiplied by a factor greater than 1, moving points farther from the x-axis.
Q2: What if the scaling factor is negative?
A2: A negative scaling factor (e.g., y = -1/2f(x)) introduces a reflection across the x-axis in addition to the vertical scaling. The graph is compressed vertically and flipped upside down.
Q3: Can this transformation be applied to piecewise functions?
A3: Yes, the transformation can be applied to piecewise functions. Each piece of the function is scaled vertically by the factor of 1/2.
Q4: How does this transformation affect the domain and range of the function?
A4: The domain of the function remains unchanged because the transformation only affects the y-values. The range, however, is scaled vertically by a factor of 1/2. If the range of f(x) is [a, b], the range of 1/2f(x) will be [a/2, b/2].
Conclusion: Mastering Function Transformations
Understanding the transformation y = 1/2f(x) is crucial for mastering function transformations. By systematically analyzing the effects of the scaling factor on key features of the parent function, you can accurately sketch the transformed graph and apply this knowledge to various mathematical contexts. Remember to focus on the vertical scaling effect, while keeping in mind how this interacts with other potential transformations and the original characteristics of the parent function f(x). Through consistent practice and a deep understanding of the underlying principles, you can confidently navigate the complexities of function transformations and their applications in various mathematical fields.
Latest Posts
Latest Posts
-
Which Phrase Completes The Diagram
Sep 14, 2025
-
Word Module 1 Sam Exam
Sep 14, 2025
-
Administrative Civil Or Criminal Sanctions
Sep 14, 2025
-
By Facilitating Trade Facilitates Specialization
Sep 14, 2025
-
1 11 Lab Input Mad Lib
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 1 2f X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.