Graph 2x 3 X 2
khabri
Sep 08, 2025 · 6 min read
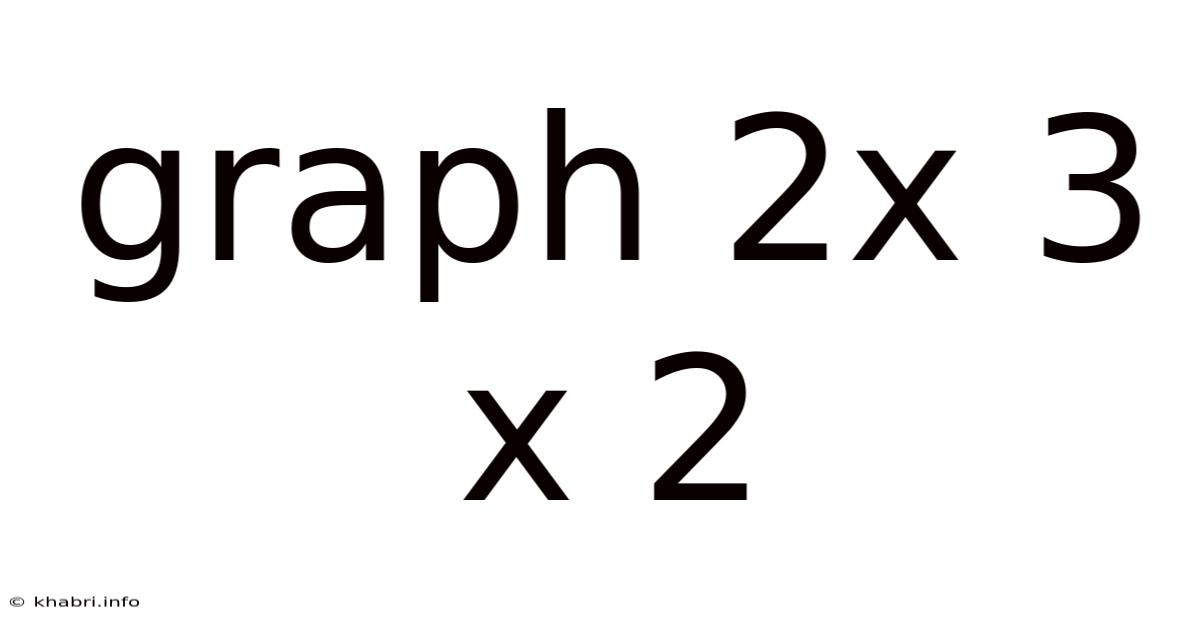
Table of Contents
Decoding the Graph of 2x³ - 3x²: A Comprehensive Guide
Understanding the graph of a polynomial function like 2x³ - 3x² is crucial for success in algebra and calculus. This seemingly simple equation hides a wealth of information about its shape, behavior, and key features. This article will provide a comprehensive guide to understanding and sketching the graph of 2x³ - 3x², covering its characteristics, key points, and the underlying mathematical principles. We will explore its behavior at infinity, find its critical points (local maxima and minima), and determine its inflection points, allowing us to accurately represent it visually.
I. Introduction: Understanding Polynomial Functions
Before diving into the specifics of 2x³ - 3x², let's briefly review some fundamental concepts regarding polynomial functions. A polynomial function is a function that can be expressed in the form:
f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₂x² + a₁x + a₀
where:
- 'n' is a non-negative integer (the degree of the polynomial).
- 'aₙ', 'aₙ₋₁', ..., 'a₀' are constants (coefficients).
The degree of the polynomial dictates many of its properties. Our function, 2x³ - 3x², is a cubic polynomial because its highest power of x is 3. Cubic polynomials have several characteristic features:
- They can have up to three real roots (x-intercepts).
- They can have up to two turning points (local maxima and minima).
- Their graph extends to positive infinity in one direction and negative infinity in the other.
Understanding these general properties provides a framework for analyzing our specific function.
II. Finding the x-Intercepts (Roots)
The x-intercepts, or roots, of the function are the values of x where the function's value (y) is zero: f(x) = 0. To find these, we set 2x³ - 3x² = 0 and solve for x:
x²(2x - 3) = 0
This equation factors nicely, giving us two roots:
- x = 0 (a root of multiplicity 2)
- x = 3/2 = 1.5
The root x = 0 has a multiplicity of 2, meaning the graph touches the x-axis at this point but doesn't cross it. The root x = 1.5 is a simple root, meaning the graph crosses the x-axis at this point.
III. Finding the y-Intercept
The y-intercept is the point where the graph intersects the y-axis, which occurs when x = 0. Substituting x = 0 into our function, we get:
f(0) = 2(0)³ - 3(0)² = 0
So, the y-intercept is at (0, 0). This confirms that the origin (0,0) is one of our x-intercepts.
IV. Determining the Critical Points (Local Maxima and Minima)
Critical points are points where the derivative of the function is zero or undefined. The derivative of 2x³ - 3x² is:
f'(x) = 6x² - 6x
Setting f'(x) = 0 to find the critical points:
6x² - 6x = 0 6x(x - 1) = 0
This gives us two critical points:
- x = 0
- x = 1
To determine whether these are local maxima or minima, we can use the second derivative test. The second derivative is:
f''(x) = 12x - 6
- For x = 0: f''(0) = -6 < 0, indicating a local maximum at x = 0.
- For x = 1: f''(1) = 6 > 0, indicating a local minimum at x = 1.
V. Finding the Inflection Point
An inflection point is a point where the concavity of the graph changes. This occurs where the second derivative is zero or undefined. We already have the second derivative:
f''(x) = 12x - 6
Setting f''(x) = 0:
12x - 6 = 0 x = 1/2 = 0.5
To confirm this is an inflection point, we can check the concavity on either side of x = 0.5. For x < 0.5, f''(x) < 0 (concave down), and for x > 0.5, f''(x) > 0 (concave up). Thus, x = 0.5 is indeed an inflection point.
VI. End Behavior of the Function
The end behavior describes how the function behaves as x approaches positive and negative infinity. Since this is a cubic polynomial with a positive leading coefficient (2), the end behavior is:
- As x → ∞, f(x) → ∞
- As x → -∞, f(x) → -∞
VII. Sketching the Graph
Now, we have all the information needed to sketch the graph:
- x-intercepts: (0, 0) and (1.5, 0)
- y-intercept: (0, 0)
- Local maximum: At x = 0, f(0) = 0
- Local minimum: At x = 1, f(1) = 2(1)³ - 3(1)² = -1 So the point is (1,-1)
- Inflection point: At x = 0.5, f(0.5) = 2(0.5)³ - 3(0.5)² = -0.25. The point is (0.5, -0.25)
- End behavior: As x goes to positive infinity, y goes to positive infinity; as x goes to negative infinity, y goes to negative infinity.
By plotting these points and considering the concavity changes around the inflection point, we can accurately sketch the graph of 2x³ - 3x². The graph will start from the bottom left, curve upwards, passing through (0,0) (touching but not crossing), reach a local minimum at (1,-1), inflect at (0.5, -0.25), and then continue to rise towards positive infinity.
VIII. Further Analysis and Applications
This detailed analysis allows us to understand the behavior of the function completely. Further applications of this understanding include:
- Solving inequalities: Determining intervals where 2x³ - 3x² is positive or negative.
- Optimization problems: Finding maximum or minimum values within specific intervals.
- Calculus applications: Using the function and its derivatives for more complex calculations, such as finding areas under the curve or volumes of revolution.
IX. Frequently Asked Questions (FAQ)
Q: What is the significance of the multiplicity of the root x = 0?
A: The multiplicity of 2 at x = 0 means the graph touches the x-axis at this point but doesn't cross it. The graph is tangent to the x-axis at (0,0).
Q: Can a cubic polynomial have only one real root?
A: Yes, a cubic polynomial can have one real root and two complex roots. However, it must have at least one real root.
Q: How can I verify my graph using a graphing calculator or software?
A: You can input the function 2x³ - 3x² into a graphing calculator or software like Desmos or GeoGebra to visually verify the graph you've sketched. This will help confirm the accuracy of your calculations.
Q: Are there other methods to find the local maxima and minima besides the second derivative test?
A: Yes, the first derivative test can also be used to determine the nature of critical points. This involves analyzing the sign of the first derivative around the critical points.
Q: What if the polynomial was more complex?
A: The same principles apply to more complex polynomials, although finding the roots might become more challenging and require numerical methods. The approach of finding derivatives, critical points, and inflection points remains the same.
X. Conclusion
Understanding the graph of 2x³ - 3x² involves a systematic approach combining algebraic manipulation, calculus techniques, and careful interpretation of the results. By systematically finding the x and y intercepts, critical points, inflection points, and analyzing the end behavior, we can accurately sketch the graph and gain a deep understanding of the function’s characteristics. This approach can be extended to analyze other polynomial functions, solidifying your grasp of fundamental mathematical concepts and their visual representations. This detailed analysis not only helps visualize the function but also lays the foundation for applying it to various mathematical and real-world problems.
Latest Posts
Latest Posts
-
Essentials Of Sociology 4th Edition
Sep 09, 2025
-
Surfactant Facilitates Alveolar Ventilation By
Sep 09, 2025
-
Ons Chemotherapy Immunotherapy Test Questions
Sep 09, 2025
-
Inquiry Into Life Sylvia Mader
Sep 09, 2025
-
Dimensional Analysis Calculating Dosages Safely
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Graph 2x 3 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.