Gcf Of 32 And 28
khabri
Sep 10, 2025 · 6 min read
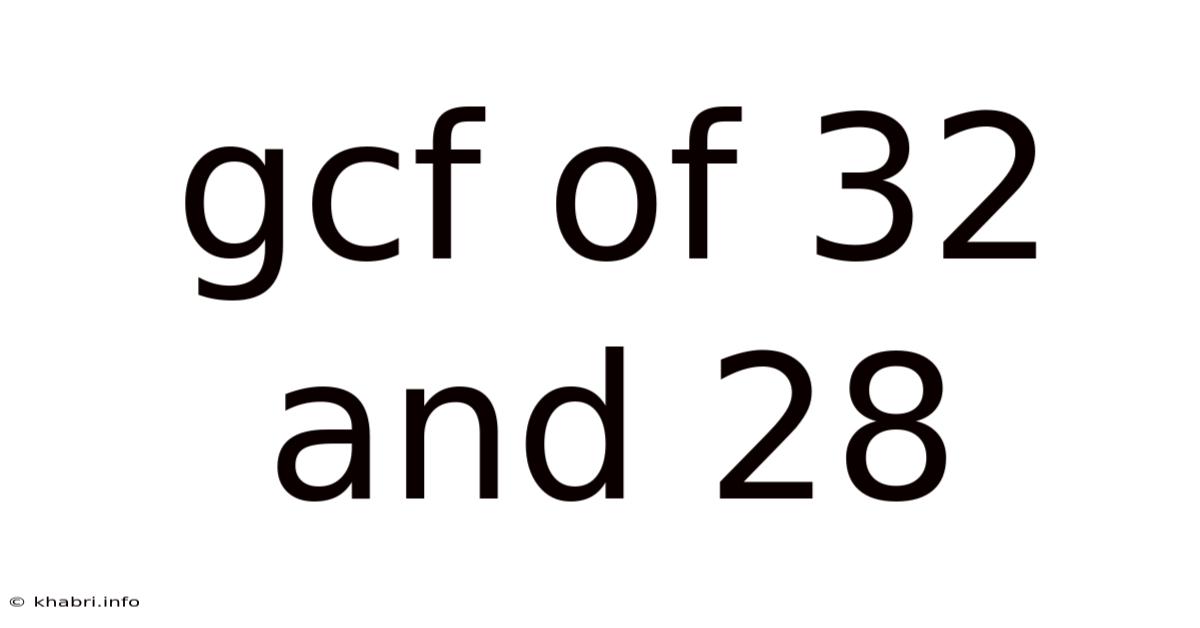
Table of Contents
Finding the Greatest Common Factor (GCF) of 32 and 28: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve into the process of determining the GCF of 32 and 28, exploring various methods and explaining the underlying mathematical principles. We'll move beyond simply finding the answer to understand why these methods work and how they can be applied to other numbers. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and building a stronger foundation in mathematics.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is a straightforward method, especially suitable for smaller numbers like 32 and 28. Let's list the factors of each number:
Factors of 32: 1, 2, 4, 8, 16, 32
Factors of 28: 1, 2, 4, 7, 14, 28
Now, we identify the common factors: 1, 2, and 4. The greatest of these common factors is 4.
Therefore, the GCF of 32 and 28 is 4.
This method is simple to visualize but can become cumbersome when dealing with larger numbers. It requires a thorough understanding of factorization and can be prone to errors if factors are missed.
Method 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This method is more efficient for larger numbers and provides a deeper understanding of the mathematical structure.
Let's find the prime factorization of 32 and 28:
Prime factorization of 32:
32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
Prime factorization of 28:
28 = 2 x 14 = 2 x 2 x 7 = 2<sup>2</sup> x 7
Now, we identify the common prime factors and their lowest powers:
Both 32 and 28 share the prime factor 2. The lowest power of 2 present in both factorizations is 2<sup>2</sup> (or 4).
Therefore, the GCF of 32 and 28 is 2<sup>2</sup> = 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to 32 and 28:
- Start with the larger number (32) and the smaller number (28).
- Subtract the smaller number from the larger number: 32 - 28 = 4
- Replace the larger number with the result (4), and keep the smaller number (28). Now we have the numbers 28 and 4.
- Repeat the subtraction: 28 - 4 = 24
- We now have 24 and 4. Repeat: 24 - 4 = 20
- We have 20 and 4. Repeat: 20 - 4 = 16
- We have 16 and 4. Repeat: 16 - 4 = 12
- We have 12 and 4. Repeat: 12 - 4 = 8
- We have 8 and 4. Repeat: 8 - 4 = 4
- We have 4 and 4. The numbers are equal, so the GCF is 4.
Therefore, the GCF of 32 and 28 is 4. The Euclidean algorithm, while seemingly lengthy in this example, becomes incredibly efficient when dealing with much larger numbers.
Explaining the Euclidean Algorithm: A Deeper Dive
The Euclidean algorithm's efficiency stems from the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. When we repeatedly subtract the smaller number from the larger number, we are essentially removing multiples of the smaller number from the larger number. This process continues until we reach a point where the remainder is 0 or the two numbers are equal. The last non-zero remainder is the GCF.
The algorithm can be expressed more concisely using the modulo operator (%). The modulo operator gives the remainder of a division. The Euclidean algorithm can be rewritten as follows:
- Let a = 32 and b = 28.
- While b ≠ 0: a = b b = a mod b
Let's trace this:
- Initially, a = 32, b = 28.
- Iteration 1: a becomes 28, b becomes 32 mod 28 = 4.
- Iteration 2: a becomes 4, b becomes 28 mod 4 = 0.
- The loop terminates because b is now 0. The GCF is the value of a, which is 4.
Applications of GCF
The GCF has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms. For example, the fraction 28/32 can be simplified to 7/8 by dividing both the numerator and denominator by their GCF, which is 4.
-
Solving Algebraic Equations: The GCF is often used in factoring algebraic expressions, which is essential for solving equations.
-
Number Theory: The GCF plays a vital role in various number theory concepts, such as modular arithmetic and cryptography.
-
Real-World Applications: GCF can be used in various real-world scenarios, such as dividing objects into equal groups or determining the size of the largest square tile that can be used to cover a rectangular floor.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they have no common factors other than 1.
-
Q: Can the GCF of two numbers be greater than the smaller number?
- A: No. The GCF is always less than or equal to the smaller of the two numbers.
-
Q: Can I use a calculator to find the GCF?
- A: Yes, many calculators, both physical and online, have built-in functions or programs to calculate the GCF.
-
Q: How do I find the GCF of more than two numbers?
- A: You can find the GCF of more than two numbers by first finding the GCF of any two of the numbers, and then finding the GCF of that result and the next number, and so on. Alternatively, you can use prime factorization; find the prime factorization of each number and then take the common prime factors raised to the lowest power.
Conclusion
Finding the greatest common factor is a crucial skill in mathematics with wide-ranging applications. We've explored three different methods – listing factors, prime factorization, and the Euclidean algorithm – each offering its unique advantages depending on the numbers involved and the level of understanding required. Mastering these methods provides a solid foundation for more advanced mathematical concepts and problem-solving skills. Remember that while the answer to the GCF of 32 and 28 is 4, the true value lies in understanding the underlying principles and the various approaches to arrive at that solution. The journey of learning is often more valuable than the destination itself.
Latest Posts
Latest Posts
-
Bar Graph Of Internet Usage
Sep 10, 2025
-
Lewis Structure For Magnesium Sulfide
Sep 10, 2025
-
Macpherson V Buick Motor Co
Sep 10, 2025
-
Histidine Charge At Ph 7
Sep 10, 2025
-
The Determinants Of Aggregate Supply
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 32 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.