Csc 2x Sqrt 2 Formula
khabri
Sep 09, 2025 · 6 min read
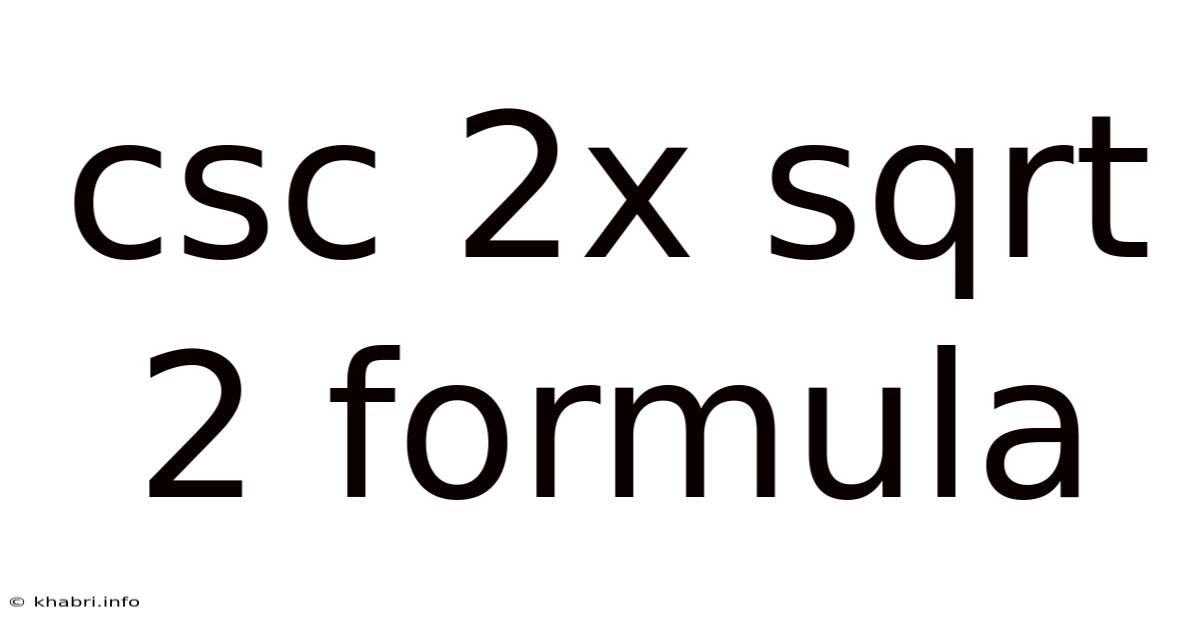
Table of Contents
Decoding the CSC 2x√2 Formula: A Deep Dive into Trigonometric Identities
The expression csc(2x√2) might seem intimidating at first glance, but understanding its underlying trigonometric principles reveals a surprisingly elegant and powerful tool for solving various mathematical problems. This article provides a comprehensive exploration of this formula, covering its derivation, applications, and related concepts, suitable for students of trigonometry and anyone interested in deepening their understanding of mathematical identities. We will delve into the intricacies of cosecant, the double angle formula, and the role of the constant √2, ensuring a thorough and insightful examination.
Understanding the Fundamentals: Cosecant and Double Angle Identities
Before tackling the csc(2x√2) formula itself, let's refresh our understanding of its core components.
Cosecant (csc): The cosecant function is the reciprocal of the sine function. Mathematically, this is expressed as:
csc(x) = 1/sin(x)
This means the cosecant of an angle is the ratio of the hypotenuse to the opposite side in a right-angled triangle. It's crucial to understand that the cosecant is undefined where the sine function is zero (i.e., at multiples of π).
Double Angle Identities: These identities relate trigonometric functions of an angle (x) to those of its double (2x). Several important double angle identities exist, including:
sin(2x) = 2sin(x)cos(x)cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)tan(2x) = (2tan(x))/(1 - tan²(x))
These identities are fundamental to simplifying and manipulating trigonometric expressions. We'll see how they play a critical role in working with csc(2x√2).
Deriving and Understanding the CSC (2x√2) Formula
There isn't a single, universally recognized "csc(2x√2) formula." The expression itself isn't a standard identity like the double angle formulas mentioned above. Instead, it represents a specific application of trigonometric principles. The key lies in understanding how we can manipulate this expression based on the context it appears in.
Let's consider possible scenarios and how we'd approach them:
Scenario 1: Simplifying Expressions
If you encounter csc(2x√2) within a larger expression, the approach depends heavily on the surrounding terms. The goal would be to simplify the expression, potentially using the following techniques:
-
Substitution: We might substitute
u = 2x√2, simplifying the expression tocsc(u). Further simplification would depend on the context of 'u'. -
Expansion using Reciprocal Identity: We can rewrite
csc(2x√2)as1/sin(2x√2). This might be useful if other terms in the expression involve sine functions. -
Angle Addition/Subtraction Formulas (if applicable): If
2x√2can be expressed as a sum or difference of simpler angles, we could use angle addition/subtraction formulas to further expand the expression.
Scenario 2: Solving Trigonometric Equations
If csc(2x√2) appears within a trigonometric equation, the solution strategy will again depend on the specific equation. Here's a general approach:
-
Isolate the Term: Isolate
csc(2x√2)on one side of the equation. -
Use Reciprocal Identity: Rewrite
csc(2x√2)as1/sin(2x√2). -
Solve for sin(2x√2): Solve the equation for
sin(2x√2). -
Inverse Sine Function: Apply the inverse sine function (
arcsin) to find possible values for2x√2. -
Solve for x: Solve for
xby dividing by2√2and considering the periodic nature of trigonometric functions. Remember that the general solution will involve adding multiples of the period.
Scenario 3: Calculus Applications
In calculus, we might encounter csc(2x√2) during differentiation or integration. The approach involves using the chain rule for differentiation or appropriate substitution techniques for integration. For example, differentiating would involve applying the chain rule:
d/dx [csc(2x√2)] = -csc(2x√2)cot(2x√2) * d/dx(2x√2) = -2√2 csc(2x√2)cot(2x√2)
The Significance of √2
The presence of √2 in the argument of the cosecant function adds another layer of complexity. The √2 itself doesn't directly lead to a simplified form, but its impact is felt when working with specific angles. For example, if we were dealing with angles that are multiples of π/4 (45 degrees), the presence of √2 might lead to some simplification due to the properties of trigonometric functions at those angles.
Practical Applications and Examples
The applications of working with expressions like csc(2x√2) are primarily within:
- Advanced Trigonometry: Solving complex trigonometric equations and identities.
- Calculus: Differentiation and integration of trigonometric functions.
- Physics and Engineering: Modeling oscillatory phenomena where trigonometric functions are essential.
Let's consider a simple example (illustrative, not directly involving the specific expression). Suppose we need to solve the equation:
sin(2x) = 1/2
-
We find the principal value:
2x = π/6 -
Considering the periodicity of sine:
2x = π/6 + 2kπor2x = 5π/6 + 2kπ, where 'k' is an integer. -
Solving for x:
x = π/12 + kπorx = 5π/12 + kπ
This demonstrates how solving trigonometric equations often involves understanding periodicity and the use of inverse functions. A similar approach would be used for equations involving csc(2x√2), albeit with additional algebraic manipulation to handle the √2 term.
Frequently Asked Questions (FAQ)
Q1: Is there a specific formula for csc(2x√2)?
A1: No, there isn't a pre-defined, standard formula specifically for csc(2x√2). It's a function that needs to be handled using the general principles of trigonometry, such as reciprocal identities, double angle formulas, and potentially angle addition/subtraction formulas, depending on the context.
Q2: How do I simplify expressions involving csc(2x√2)?
A2: Simplification depends heavily on the entire expression. Start by using the reciprocal identity (csc(x) = 1/sin(x)), substituting variables if helpful, and exploring potential application of other trigonometric identities, including double angle formulas and angle addition/subtraction formulas.
Q3: What is the role of √2 in this expression?
A3: The √2 in csc(2x√2) doesn't simplify the expression in a direct way. However, its presence might lead to simplifications in specific contexts, particularly when dealing with angles that are multiples of π/4 (45 degrees), due to the properties of trigonometric functions at these angles.
Q4: Can I use a calculator to evaluate csc(2x√2)?
A4: Yes, you can use a scientific calculator or mathematical software to evaluate csc(2x√2) for a specific value of x. Remember to set your calculator to radians or degrees as appropriate.
Conclusion
While there’s no single, standalone "csc(2x√2) formula," understanding this expression hinges on mastering fundamental trigonometric principles: cosecant as the reciprocal of sine, double angle identities, and the ability to strategically apply these identities within the broader context of an equation or expression. The presence of √2 adds complexity, highlighting the need for careful algebraic manipulation and a deep understanding of trigonometric functions' behavior. By employing a systematic approach involving substitutions, reciprocal identities, and appropriate trigonometric formulas, one can effectively tackle problems involving this expression and develop a more nuanced understanding of advanced trigonometry. Remember to always check for potential simplifications based on the specific context in which the expression appears.
Latest Posts
Latest Posts
-
Business Communication Today 14th Edition
Sep 09, 2025
-
Nominal Gdp Real Gdp X 100
Sep 09, 2025
-
Principles Of Athletic Training Book
Sep 09, 2025
-
Stoichiometry Murder Mystery Answer Key
Sep 09, 2025
-
Richela Is A Successful Artist
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Csc 2x Sqrt 2 Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.