8 13 10 15 18
khabri
Sep 10, 2025 · 6 min read
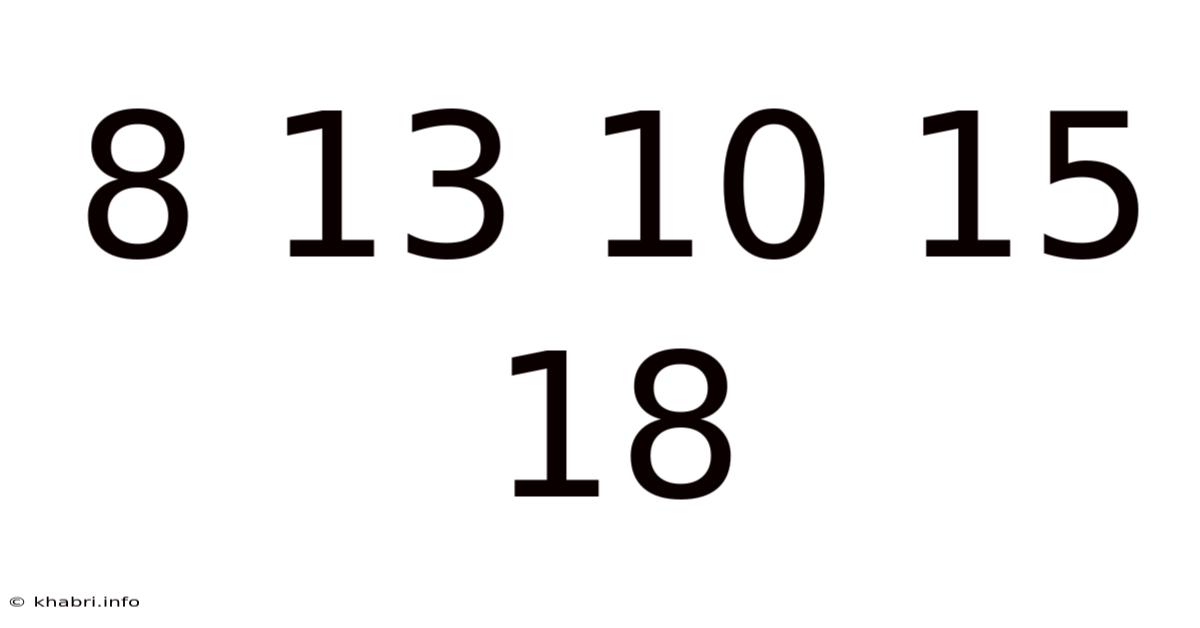
Table of Contents
Unlocking the Secrets of the Sequence: 8 13 10 15 18 – A Deep Dive into Pattern Recognition and Mathematical Reasoning
This article delves into the seemingly simple sequence: 8, 13, 10, 15, 18. While it might appear straightforward at first glance, this numerical sequence offers a rich opportunity to explore various mathematical concepts, including pattern recognition, sequence analysis, and the importance of considering multiple perspectives. We’ll unpack the sequence, revealing potential underlying patterns and exploring different approaches to understanding its structure. By the end, you’ll not only understand this specific sequence but also gain valuable skills in analyzing and interpreting numerical patterns.
Understanding the Challenge: Why This Sequence Matters
The sequence 8, 13, 10, 15, 18 presents a unique challenge because it doesn't immediately yield to a single, obvious pattern. Unlike arithmetic sequences (with a constant difference) or geometric sequences (with a constant ratio), this sequence requires a more nuanced approach. This ambiguity is precisely what makes it a valuable learning tool. It teaches us that there might not always be one "right" answer and that understanding a mathematical problem often requires creativity and the consideration of multiple possible solutions. The ability to identify patterns, whether simple or complex, is a crucial skill in various fields, from data analysis and programming to cryptography and scientific research.
Method 1: Analyzing Alternating Subsequences
One way to approach this sequence is to break it down into two alternating subsequences:
- Subsequence 1 (odd-numbered terms): 8, 10, 18
- Subsequence 2 (even-numbered terms): 13, 15
Analyzing these subsequences separately reveals potential patterns within each. Subsequence 2 shows a clear arithmetic progression with a common difference of 2. Subsequence 1, however, is less straightforward. The difference between 8 and 10 is 2, while the difference between 10 and 18 is 8. This suggests a more complex pattern or perhaps a different underlying rule altogether within this subsequence. It might be tempting to assume there's a simple pattern missing, but this initial analysis highlights the complexity of the sequence and the need for further investigation.
Method 2: Exploring Differences and Second Differences
Another common technique in sequence analysis is to examine the differences between consecutive terms. Let's calculate the first differences:
- 13 - 8 = 5
- 10 - 13 = -3
- 15 - 10 = 5
- 18 - 15 = 3
The first differences (5, -3, 5, 3) don't reveal a consistent pattern. Let's try calculating the second differences (differences between the first differences):
- -3 - 5 = -8
- 5 - (-3) = 8
- 3 - 5 = -2
Again, no immediately obvious pattern emerges. This lack of a clear pattern in the first and second differences suggests that the sequence might not be based on a simple polynomial relationship. This reinforces the idea that we need to explore alternative approaches.
Method 3: Considering Modular Arithmetic
A more advanced technique involves considering modular arithmetic. We might look for patterns within the remainders when the terms are divided by a specific number. For example, let's consider the remainders when dividing each term by 5:
- 8 % 5 = 3
- 13 % 5 = 3
- 10 % 5 = 0
- 15 % 5 = 0
- 18 % 5 = 3
Interestingly, we see a pattern in the remainders: 3, 3, 0, 0, 3. This suggests a potential cyclic pattern or relationship with multiples of 5. However, this pattern alone doesn't fully define the sequence; it only provides a partial insight. This highlights that modular arithmetic can be a valuable tool, but it often needs to be combined with other methods to fully understand the underlying structure.
Method 4: Introducing a Multi-Rule System
Perhaps the most likely explanation for the sequence lies in a system involving multiple rules or patterns operating in conjunction. For example, it's conceivable that the sequence follows one rule for odd-numbered terms and a different rule for even-numbered terms, as hinted at in Method 1. Or, there might be a more intricate rule set based on combining or altering aspects of both subsequences or other mathematical operations. The lack of a singular, easily identifiable pattern strongly suggests that the sequence might not be generated by a single, simple mathematical function. The beauty of this complexity is that it demonstrates the possibilities of creating sequences from interwoven rules.
The Importance of Context: The Missing Piece of the Puzzle
It's crucial to acknowledge that without additional context or information, definitively pinpointing the "correct" pattern for this sequence is impossible. The sequence, as presented, is open to interpretation. It could be a snippet from a much larger sequence, the result of a specific algorithm, or even a randomly generated set of numbers. The lack of context highlights a critical aspect of mathematical problem-solving: the importance of understanding the origin or purpose of the data being analyzed.
Expanding the Possibilities: Generating Extensions
While we can’t definitively identify the underlying rule, we can explore potential extensions of the sequence based on the patterns we've observed. For example, if we assume the even-numbered terms continue their arithmetic progression (adding 2 each time), and the odd-numbered terms follow a more complex pattern (perhaps involving additions based on prime numbers or other mathematical functions), we could generate possible extensions. This exercise demonstrates the power of hypothesising and testing different patterns, even when a definitive answer is unavailable.
Addressing Potential Objections and Alternative Interpretations
Someone might argue that the sequence is simply random, and there is no underlying pattern. While this is a valid possibility, the exploration itself holds educational value. Even in the absence of a clear pattern, the process of examining the sequence strengthens analytical skills. The attempts to find patterns teach us how to approach data systematically, test hypotheses, and appreciate the complexity and sometimes ambiguity inherent in mathematical analysis.
Others might suggest different methods to approach this sequence, including advanced mathematical techniques. The variety of perspectives and approaches is what makes this kind of problem so rich. There isn't a single "right" way to analyze a sequence; the value lies in exploring multiple avenues and developing a deeper understanding of various mathematical concepts.
Conclusion: The Enduring Lesson of 8 13 10 15 18
The seemingly simple sequence 8, 13, 10, 15, 18 offers a profound lesson in mathematical exploration. It highlights the importance of pattern recognition, the need to consider multiple perspectives, and the limitations of relying on single, simple solutions. The ambiguity of the sequence underscores the beauty of mathematical thinking: the continuous questioning, exploration, and refinement of hypotheses. Whether or not a definitive pattern exists, the process of analyzing this sequence cultivates critical thinking skills and fosters a deeper appreciation for the intricacies and subtleties of mathematics. This problem serves as an excellent exercise in demonstrating the iterative nature of problem-solving and the power of a multi-faceted approach to data analysis. The enduring lesson is not necessarily the "answer" but the journey of exploration itself.
Latest Posts
Latest Posts
-
Choose The Functions Of Microtubules
Sep 10, 2025
-
When Do Bytes Become Meaningful
Sep 10, 2025
-
Rearrange Expression Into Quadratic Form
Sep 10, 2025
-
2 Bromo 4 Methylpentane Stereoisomers
Sep 10, 2025
-
1 3 Piecewise Functions Homework Answers
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 8 13 10 15 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.