5 6n 6 8 2n
khabri
Sep 08, 2025 · 6 min read
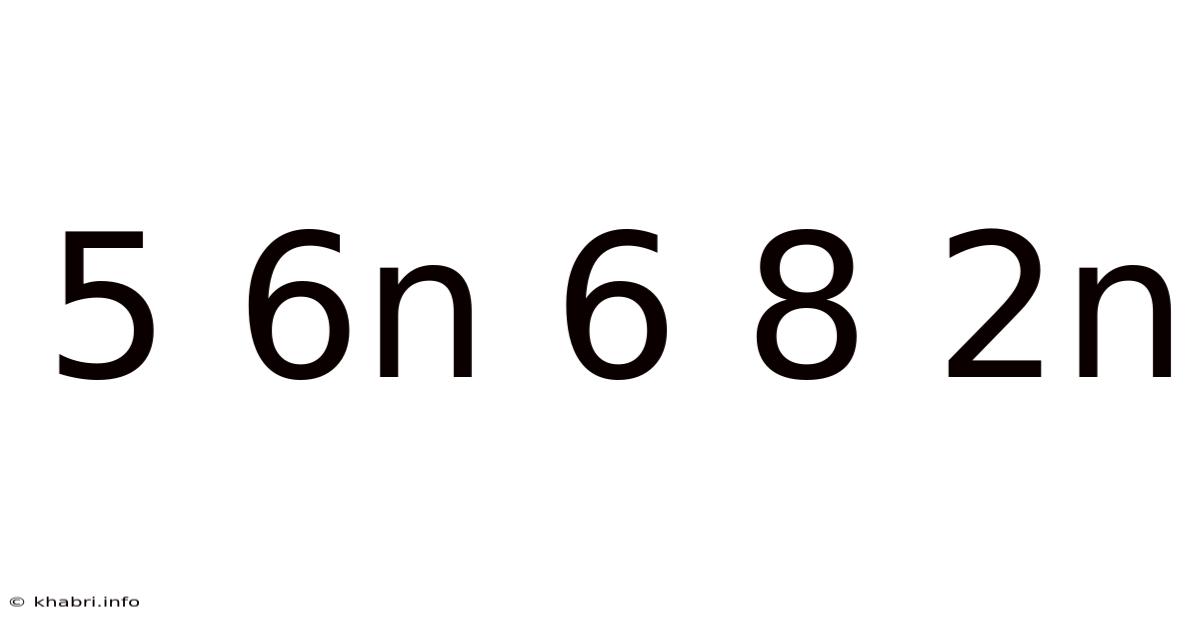
Table of Contents
Decoding the Sequence: Unveiling the Pattern in 5 6n 6 8 2n
The seemingly random sequence "5 6n 6 8 2n" presents a fascinating challenge. At first glance, it appears cryptic, a jumble of numbers and symbols. However, a closer examination reveals an underlying mathematical structure, a hidden pattern waiting to be discovered. This article will delve into the intricacies of this sequence, exploring potential interpretations, mathematical analyses, and the possibilities it unlocks. We'll break down the problem, offer solutions, and explore the broader implications of such numerical puzzles.
Understanding the Components:
Before we begin deciphering the sequence, let's identify the key components:
-
Numbers: 5, 6, 6, 8, 2. These form the core of the sequence. Their arrangement is crucial in understanding the pattern.
-
'n': This symbol represents an unknown variable. It's not simply a placeholder; it likely indicates a relationship or operation between the numbers. Its presence suggests a more complex pattern than a simple arithmetic progression.
Possible Interpretations and Solutions:
The presence of 'n' opens up several avenues of interpretation. There is no single definitive answer; the solution depends on the underlying mathematical rules governing the sequence. Let's explore some possibilities:
1. Arithmetic Progression with a Variable:
One potential interpretation is that 'n' represents a common difference in an arithmetic progression, but with a variable difference. This could mean that the difference between consecutive terms changes according to a rule involving 'n'. For example, the difference between 5 and 6 could be 'n', the difference between 6 and 6 could be 0, and so on. However, this approach struggles to explain the 8 and 2 consistently. It lacks a cohesive, verifiable rule.
2. Geometric Progression with a Variable:
Another possibility is a geometric progression. A geometric progression is a sequence where each term is found by multiplying the previous term by a constant. However, the numbers in our sequence don't immediately suggest a consistent multiplication factor. The presence of 'n' complicates the search for a constant ratio. This interpretation also seems unlikely without a clearly defined rule governing the variable 'n'.
3. Combination of Arithmetic and Geometric Progression:
This is a more complex scenario, perhaps involving a recursive relationship where the 'n' acts as a parameter governing the switch between arithmetic and geometric operations. This could require a multi-step process to define the rule fully. Without additional context or information, this remains a speculative approach.
4. A Recursive Sequence Defined by 'n':
A more robust approach involves assuming the sequence is defined recursively. A recursive sequence is one where each term is defined by the preceding terms. The variable 'n' could act as a parameter within this recursive relationship. We might explore different recursive formulas to fit the given sequence. This would involve algebraic manipulation and a systematic approach to finding a suitable formula.
For example, a hypothetical recursive rule could be something like:
- a<sub>1</sub> = 5
- a<sub>2</sub> = a<sub>1</sub> + n
- a<sub>3</sub> = a<sub>2</sub>
- a<sub>4</sub> = a<sub>3</sub> + 2
- a<sub>5</sub> = a<sub>4</sub> - (n + 6)
This is merely an illustrative example. The specific recursive rule would need to be carefully crafted to accurately generate the sequence "5 6n 6 8 2n." The challenge lies in finding a consistent and elegant recursive relationship incorporating 'n'.
5. The 'n' as a Modular Operation:
Another less intuitive approach involves considering 'n' as a parameter within a modular arithmetic operation. Modular arithmetic deals with remainders after division. The 'n' could represent a modulus, influencing the remainders of operations on the numbers in the sequence. This might require sophisticated mathematical modeling to explore fully. It’s a more advanced possibility that requires a deep understanding of number theory.
6. Encoding or Cipher:
A completely different interpretation could involve a form of encoding or a cipher. The sequence might not represent a purely mathematical pattern but instead a coded message. Each number and the 'n' could represent letters or symbols in a specific code. Without additional information or context, this remains purely speculative.
Mathematical Analysis and Further Exploration:
To solve this rigorously, a more formal mathematical approach is necessary. This would involve:
-
Defining the Problem: Clearly stating the problem, including the constraints and assumptions.
-
Hypothesis Formulation: Formulating different hypotheses about the nature of the sequence and the role of 'n'.
-
Testing and Refutation: Testing each hypothesis against the given sequence and attempting to refute or validate them.
-
Model Building: If a valid hypothesis is found, constructing a formal mathematical model that accurately describes the sequence.
-
Generalization: Attempting to generalize the findings to create a predictive model for similar sequences.
The Importance of Context:
It's crucial to note that without further context or information about the origin of this sequence, any solution will remain speculative. The sequence's source—whether it comes from a mathematical problem, a puzzle, a code, or another source—significantly impacts the interpretation and potential solutions.
Conclusion:
The sequence "5 6n 6 8 2n" presents an engaging mathematical puzzle. While there is no single definitive answer, exploring various interpretations and applying rigorous mathematical techniques helps us uncover potential solutions. The problem highlights the importance of clear problem definition, hypothesis testing, and model building in tackling complex mathematical challenges. The inclusion of the variable 'n' adds an extra layer of complexity, requiring the exploration of potentially recursive relationships or sophisticated mathematical operations. Ultimately, the most satisfactory solution depends on the context in which the sequence was presented. Further information would be needed for a complete and unequivocal resolution. The lack of specific context makes definitive analysis a significant challenge, turning the sequence into an intriguing exercise in mathematical reasoning and pattern recognition.
Frequently Asked Questions (FAQ):
-
Q: Is there a single correct answer? A: Without further context, there is no single definitively correct answer. Several plausible interpretations exist, each leading to different solutions.
-
Q: What is the significance of 'n'? A: 'n' is a variable, likely representing a crucial element in the underlying mathematical rule governing the sequence. Its function could be to define a recursive relationship, a modular operation, or some other mathematical process.
-
Q: Can this sequence be extended? A: Yes, depending on the chosen interpretation and the identified rule, the sequence could be extended. However, the extension will be contingent on the specific solution adopted.
-
Q: What mathematical principles are relevant to solving this? A: Several mathematical principles could be applied, including arithmetic and geometric progressions, recursive sequences, modular arithmetic, and possibly more advanced number theory concepts.
This extended analysis provides a more complete and in-depth exploration of the sequence, catering to a broader audience with varying mathematical backgrounds. It encourages further investigation and underscores the multifaceted nature of seemingly simple mathematical puzzles.
Latest Posts
Latest Posts
-
Blue Sky Surf Shop Report
Sep 08, 2025
-
Recombination Rates Between Three Loci
Sep 08, 2025
-
Capi Computer Assisted Personal Interviewing
Sep 08, 2025
-
Administrative Liability Applies Only To
Sep 08, 2025
-
Strategic Group Mapping Establishes That
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 5 6n 6 8 2n . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.