4x 3y - 4y 10x
khabri
Sep 07, 2025 · 5 min read
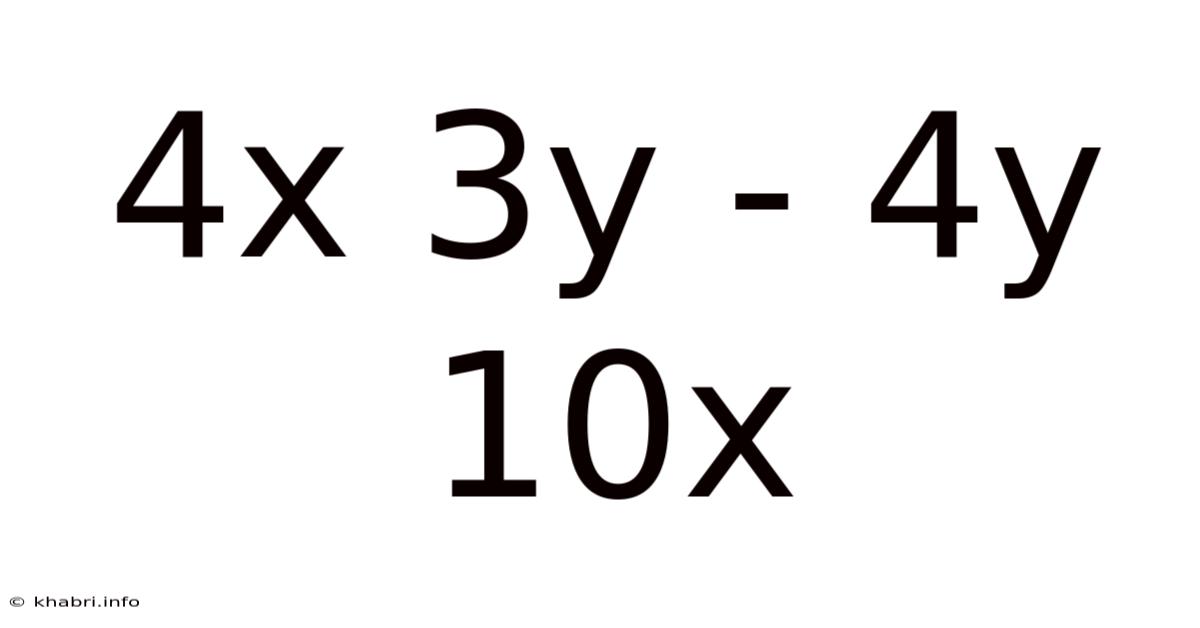
Table of Contents
Simplifying and Solving Algebraic Expressions: A Deep Dive into 4x + 3y - 4y + 10x
This article provides a comprehensive guide to understanding and simplifying the algebraic expression 4x + 3y - 4y + 10x. We'll break down the process step-by-step, exploring the underlying principles of algebra and demonstrating how to solve similar problems. Whether you're a beginner grappling with basic algebraic concepts or looking to refresh your knowledge, this guide will equip you with the necessary skills and understanding. We will cover simplifying the expression, solving for variables (given certain conditions), and even explore some common mistakes to avoid. This detailed explanation will ensure a firm grasp of this fundamental algebraic concept.
Understanding the Basics: Terms, Variables, and Coefficients
Before we delve into simplifying the expression 4x + 3y - 4y + 10x, let's review some fundamental algebraic terms. An algebraic expression is a mathematical phrase that combines numbers, variables, and operations. In our expression, 'x' and 'y' are variables, representing unknown quantities. The numbers preceding the variables are called coefficients. For example, in the term 4x, '4' is the coefficient of 'x'. Finally, the individual parts of an expression separated by plus or minus signs are called terms. Our expression has four terms: 4x, 3y, -4y, and 10x.
Simplifying the Expression: Combining Like Terms
The key to simplifying the expression 4x + 3y - 4y + 10x lies in combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, we have two types of like terms: terms with 'x' and terms with 'y'.
Let's group the like terms together:
(4x + 10x) + (3y - 4y)
Now, we can simplify each group by adding or subtracting the coefficients:
4x + 10x = 14x
3y - 4y = -y
Therefore, the simplified expression is:
14x - y
This is the most simplified form of the original expression. We cannot combine 14x and -y further because they are unlike terms (they have different variables).
Solving for Variables: A Deeper Dive
While simplifying the expression gives us a more concise form (14x - y), we can go further if we have additional information. To solve for a variable, we need an equation—a statement that two expressions are equal. Let's explore some scenarios:
Scenario 1: Finding x if y is known
Let's assume we know the value of y. For example, let's say y = 5. We can substitute this value into our simplified expression:
14x - y = 14x - 5
To solve for x, we need another equation relating x and y. Suppose we know that the entire expression is equal to 20:
14x - 5 = 20
Now we can solve for x using basic algebraic techniques:
- Add 5 to both sides: 14x = 25
- Divide both sides by 14: x = 25/14
Therefore, if y = 5 and the expression equals 20, then x = 25/14.
Scenario 2: Finding y if x is known
Similarly, if we know the value of x, we can substitute it into the simplified expression and solve for y. Let's assume x = 2 and the expression equals 26:
14x - y = 26
Substitute x = 2:
14(2) - y = 26
28 - y = 26
Subtract 28 from both sides:
-y = -2
Multiply both sides by -1:
y = 2
Therefore, if x = 2 and the expression equals 26, then y = 2.
Scenario 3: Solving a System of Equations
Solving for both x and y requires a system of two equations. For example:
Equation 1: 14x - y = 20 Equation 2: x + y = 10
We can use various methods to solve this system, such as substitution or elimination. Using elimination, we can add the two equations together:
(14x - y) + (x + y) = 20 + 10
This simplifies to:
15x = 30
x = 2
Now, substitute x = 2 into either Equation 1 or Equation 2 to solve for y. Using Equation 2:
2 + y = 10
y = 8
Therefore, the solution to the system of equations is x = 2 and y = 8.
Explanation of the Algebraic Principles
The simplification process relies on the distributive property and the commutative property of addition.
-
Distributive Property: This property states that a(b + c) = ab + ac. While not explicitly used in simplifying this particular expression, it's crucial for understanding more complex algebraic manipulations.
-
Commutative Property of Addition: This property states that a + b = b + a. This allows us to rearrange the terms in the expression to group like terms together without changing the overall value.
Common Mistakes to Avoid
Several common mistakes can arise when simplifying algebraic expressions:
-
Incorrectly combining unlike terms: Remember, you can only combine terms that have the same variable raised to the same power. Adding 4x and 3y to get 7xy is incorrect.
-
Errors in sign manipulation: Pay close attention to the signs (+ or -) before each term. A common error is forgetting to distribute a negative sign correctly.
-
Arithmetic errors: Carefully perform the addition and subtraction of coefficients. Double-checking your calculations is always a good idea.
Frequently Asked Questions (FAQ)
Q: Can I simplify the expression in a different order?
A: Yes, the commutative property of addition allows you to rearrange the terms before grouping like terms. The final simplified expression will remain the same.
Q: What if the expression had exponents?
A: If the expression included terms with exponents (e.g., x², y³), you would only be able to combine like terms with the same variable and the same exponent. For example, 2x² and 5x² are like terms, but 2x² and 5x are not.
Q: What if there were more variables?
A: The same principles apply. Group like terms with the same variables and exponents, and then combine the coefficients.
Q: Why is simplification important?
A: Simplifying expressions makes them easier to understand, work with, and solve. It is a fundamental step in many algebraic processes.
Conclusion
Simplifying the algebraic expression 4x + 3y - 4y + 10x involves combining like terms to obtain the simplified form 14x - y. This process utilizes the commutative and distributive properties of algebra. Solving for variables requires additional information in the form of an equation or a system of equations. Understanding the basic principles and avoiding common mistakes will ensure success in simplifying and solving algebraic expressions. This fundamental skill is crucial for progressing in mathematics and various fields that rely on mathematical modeling and problem-solving. Remember to practice regularly to build your confidence and proficiency.
Latest Posts
Latest Posts
-
A Crystal Of Nacl Is
Sep 07, 2025
-
The Labor Contract Is Signed
Sep 07, 2025
-
Can Kinetic Energy Be Negative
Sep 07, 2025
-
3 Topic Assessment Form B
Sep 07, 2025
-
Initial Knowledge Check Aleks Answers
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 4x 3y - 4y 10x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.