40 Divided By 5 -4
khabri
Sep 15, 2025 · 6 min read
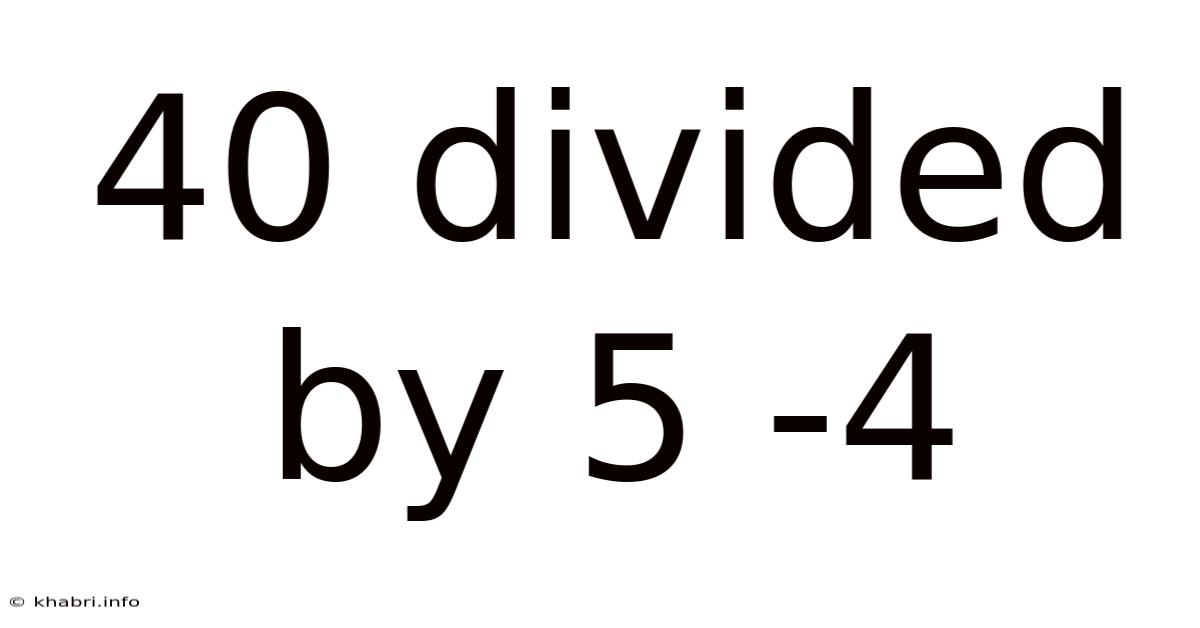
Table of Contents
Unveiling the Mystery: A Deep Dive into 40 Divided by 5 Minus 4
This article will explore the seemingly simple mathematical expression "40 divided by 5 minus 4," delving beyond the immediate answer to uncover the underlying principles and broader applications of arithmetic operations. We'll break down the problem step-by-step, discuss the order of operations (PEMDAS/BODMAS), examine the concept of division and subtraction, and even touch upon the historical context of these fundamental mathematical tools. This comprehensive guide is designed for learners of all levels, from those just beginning their mathematical journey to those looking to refresh their foundational knowledge.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before tackling the problem directly, it's crucial to understand the order of operations. This set of rules ensures consistency in evaluating mathematical expressions. The acronyms PEMDAS and BODMAS are commonly used to remember the order:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- BODMAS: Brackets, Orders, Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Both acronyms represent the same order of operations; the difference lies in the terminology used. "Parentheses" and "Brackets" are synonymous, as are "Exponents" and "Orders." The key takeaway is that we must perform operations within parentheses first, followed by exponents, then multiplication and division (working from left to right if both appear), and finally addition and subtraction (also from left to right if both appear).
Step-by-Step Solution to 40 Divided by 5 Minus 4
Now, let's apply the order of operations to solve "40 divided by 5 minus 4":
-
Division: The first operation is division. 40 divided by 5 is 8. Our expression now becomes: 8 - 4.
-
Subtraction: The next operation is subtraction. 8 minus 4 is 4.
Therefore, the final answer to the expression "40 divided by 5 minus 4" is 4.
A Deeper Dive into Division
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. It's the inverse of multiplication. When we say "40 divided by 5," we're asking: "How many times does 5 go into 40?" The answer, as we've seen, is 8. This can be visually represented using various methods, such as:
-
Repeated Subtraction: Subtracting 5 from 40 repeatedly until we reach 0. We would subtract 5 eight times, confirming that 5 goes into 40 eight times.
-
Arrays/Groups: Imagine arranging 40 objects into groups of 5. We'd have 8 groups.
-
Fraction Representation: The expression "40 divided by 5" can be represented as the fraction 40/5, which simplifies to 8.
Understanding division at this deeper level is crucial for grasping more complex mathematical concepts later on, such as fractions, ratios, and proportions.
A Deeper Dive into Subtraction
Subtraction is another fundamental arithmetic operation involving finding the difference between two numbers. In our problem, we subtracted 4 from 8. This represents taking away 4 units from a total of 8 units. Like division, subtraction has various real-world applications:
-
Calculating Differences: Determining the difference in temperature, height, weight, or any measurable quantity.
-
Finding Remaining Quantities: Determining the amount left after spending or consuming a certain quantity.
-
Problem Solving: Subtraction is integral to solving countless word problems involving comparisons and reductions.
Understanding the nuances of subtraction helps build a stronger foundation for algebra and other higher-level mathematical concepts.
The Importance of Parentheses and Brackets
While our example didn't include parentheses, their presence would significantly alter the outcome. Let's consider a slightly modified expression: (40 divided by 5) - 4 and 40 divided by (5 - 4).
-
(40 divided by 5) - 4: Here, the parentheses dictate that the division must be performed before the subtraction. This leads to the same result as our original problem: (8) - 4 = 4.
-
40 divided by (5 - 4): In this case, the parentheses prioritize the subtraction. First, we calculate 5 - 4 = 1. Then, we perform the division: 40 divided by 1 = 40. This highlights the crucial role of parentheses in determining the order of operations and, subsequently, the final answer.
Real-World Applications: Beyond the Classroom
The principles involved in solving "40 divided by 5 minus 4" aren't confined to the abstract world of mathematics. They have practical applications across numerous fields:
-
Finance: Calculating profits, losses, and balances. Dividing expenses among multiple people and subtracting taxes from income are just a few examples.
-
Engineering: Designing structures, calculating distances, and determining quantities of materials.
-
Cooking and Baking: Measuring ingredients and adjusting recipes based on the number of servings.
-
Everyday Life: Sharing items equally, calculating change, or determining the amount of time remaining.
The ability to perform these basic operations accurately and efficiently is crucial for navigating everyday life and tackling more complex challenges.
Expanding on the Concept: Introducing Variables and Equations
Let's introduce algebraic concepts to further enrich our understanding. We can rewrite the expression using variables:
Let 'x' represent the result of 40 divided by 5, and 'y' represent the final answer. Then, our problem becomes:
x = 40 / 5 y = x - 4
Solving for x and then y yields the same result: x = 8 and y = 4.
This simple example lays the foundation for understanding more complex equations and problem-solving in algebra. It demonstrates how basic arithmetic operations are building blocks for higher-level mathematical concepts.
Historical Context: A Journey Through Time
The operations of division and subtraction have ancient roots, with evidence suggesting their usage in various civilizations thousands of years ago. Ancient Egyptians used a form of division based on doubling and halving, while the Babylonians developed sophisticated methods for solving complex mathematical problems, including those involving division and subtraction. The development of these operations was gradual, with improvements and refinements over centuries, culminating in the concise and universally understood methods we use today.
Frequently Asked Questions (FAQ)
Q: What happens if I change the order of operations?
A: Changing the order of operations will almost always lead to an incorrect answer. The order of operations is essential for ensuring consistency and accuracy in evaluating mathematical expressions.
Q: Why is the order of operations important?
A: The order of operations ensures that everyone gets the same answer when evaluating the same mathematical expression. Without a standard order, multiple interpretations and answers would be possible, leading to confusion and inaccuracies.
Q: Are there any exceptions to the order of operations?
A: The order of operations is a fundamental rule. There are no exceptions, but parentheses/brackets allow you to override the standard order for specific parts of an expression.
Q: How can I improve my skills in arithmetic?
A: Practice is key! Solve a variety of problems regularly, focusing on understanding the underlying principles rather than simply memorizing steps. Consider using online resources, workbooks, or seeking help from a tutor.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "40 divided by 5 minus 4" provides a gateway to understanding the fundamental principles of arithmetic and the crucial role of the order of operations. By breaking down the problem step-by-step, we've not only found the answer (4) but also explored the deeper meaning and broader applications of division and subtraction. Mastering these foundational concepts is essential for success in more advanced mathematics and countless real-world applications. The key is consistent practice and a focus on understanding the "why" behind the "how." Remember, even the most complex mathematical concepts are built upon these fundamental building blocks. So, embrace the challenge, practice regularly, and watch your mathematical skills flourish!
Latest Posts
Latest Posts
-
What Is A Replication Bubble
Sep 15, 2025
-
Molar Mass Of Helium Gas
Sep 15, 2025
-
Is Naoch2ch3 A Strong Base
Sep 15, 2025
-
Cross Sectional Area Of Solenoid
Sep 15, 2025
-
Concept Map Of Integumentary System
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 40 Divided By 5 -4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.