2xy X 2y Algebra Tiles
khabri
Sep 12, 2025 · 6 min read
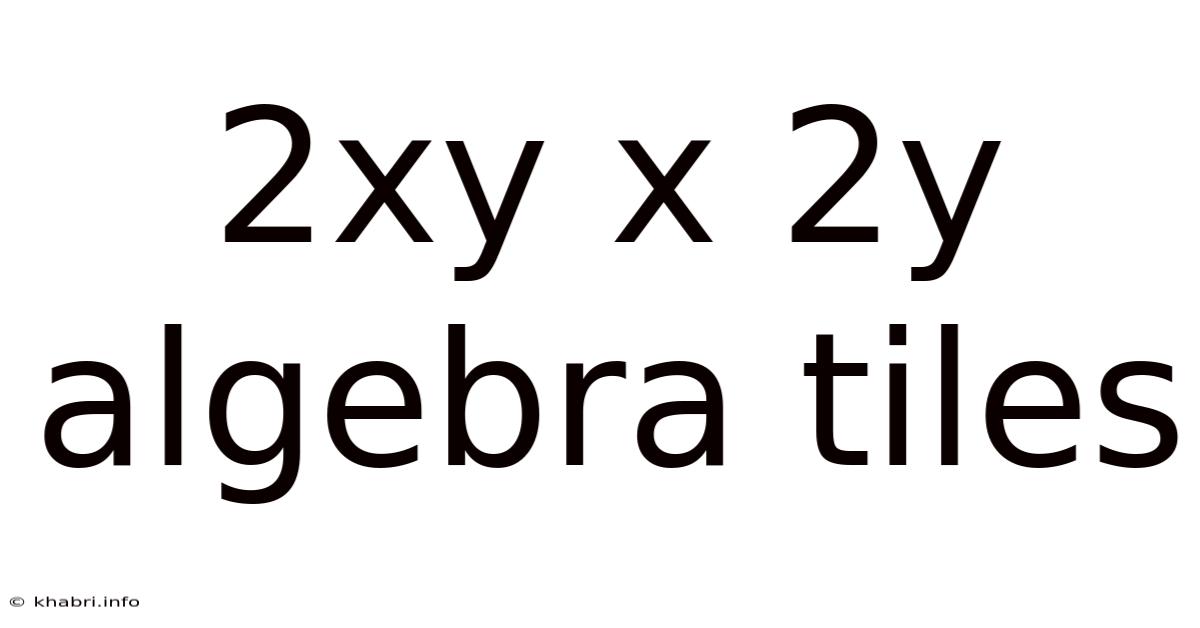
Table of Contents
Mastering Algebra: A Deep Dive into 2xy x 2y Using Algebra Tiles
Understanding algebraic manipulation can sometimes feel like navigating a maze. But with the right tools and approach, conquering even complex expressions like multiplying 2xy by 2y becomes surprisingly straightforward. This article will guide you through the process of solving 2xy x 2y using algebra tiles, a visual and hands-on method that makes abstract concepts tangible. We'll delve into the underlying principles, explore different approaches, and answer frequently asked questions to ensure a comprehensive understanding.
Introduction to Algebra Tiles
Algebra tiles are a fantastic learning tool used to visually represent algebraic expressions. They provide a concrete representation of abstract concepts, making it easier to grasp the mechanics of algebraic operations like addition, subtraction, multiplication, and division. These tiles typically come in three shapes:
- Squares: Represent constant terms (e.g., 1, 4, -9). A large square might represent x², while a smaller one represents 1.
- Rectangles: Represent variables (e.g., x, y, xy). A rectangle might represent x or y, depending on its dimensions relative to the square representing 1. A larger rectangle might represent xy.
- Small squares: These represent the unit value, often 1.
By manipulating these tiles, you can visualize the relationships between terms and perform operations in a more intuitive manner, leading to a stronger understanding of algebraic principles.
Visualizing 2xy x 2y with Algebra Tiles
Let's break down the expression 2xy x 2y using algebra tiles. We need to represent each component visually:
1. Representing 2xy:
Imagine a rectangle representing xy. To represent 2xy, we need two of these xy rectangles.
2. Representing 2y:
Now, we need to represent 2y. This would be represented by two rectangles, each representing 'y'.
3. Performing the Multiplication:
The multiplication 2xy x 2y is essentially asking: "What do we get when we combine 2xy groups, each consisting of two 'y' rectangles?"
To visualize this, we arrange our tiles: We have two xy rectangles (representing 2xy) and we need to multiply each by the two y rectangles. This effectively means arranging the two 'y' rectangles alongside each of the two xy rectangles.
This arrangement creates a larger rectangular area. The dimensions of this larger rectangle provide the answer. We observe that the larger rectangle has dimensions of 2x and 2y². Therefore, the area of this larger rectangle represents the product of 2xy and 2y.
The Mathematical Explanation
While the visual approach with algebra tiles is beneficial for understanding, it's crucial to grasp the underlying mathematical principles. The expression 2xy x 2y can be simplified using the rules of exponents and multiplication:
-
Rearrange the terms: We can rewrite the expression as: 2 * x * y * 2 * y
-
Group like terms: Group the numerical coefficients and the variables separately: (2 * 2) * (x) * (y * y)
-
Multiply the coefficients: 2 * 2 = 4
-
Simplify the variables: y * y = y² (Recall that multiplying variables with the same base means adding their exponents; y¹ * y¹ = y¹⁺¹ = y²)
-
Combine the results: Combining the results from steps 3 and 4 gives us the final answer: 4xy²
Therefore, 2xy x 2y = 4xy²
Different Approaches to Solving 2xy x 2y
While algebra tiles offer a powerful visual approach, let's examine alternative methods for solving this algebraic expression:
Method 1: The Distributive Property
While not directly applicable in this specific case (as there's no addition or subtraction involved), understanding the distributive property is crucial for more complex algebraic expressions. The distributive property states that a(b + c) = ab + ac. This helps simplify expressions where a term is multiplied by a sum or difference.
Method 2: Using the Commutative and Associative Properties
The commutative property states that the order of multiplication doesn't affect the result (a x b = b x a). The associative property states that the grouping of numbers in multiplication doesn't affect the result (a x (b x c) = (a x b) x c). We used these implicitly in the earlier algebraic method when rearranging and grouping terms.
Method 3: Direct Multiplication
The most straightforward approach is to multiply the coefficients and variables directly. This involves multiplying the numerical coefficients (2 x 2 = 4) and then multiplying the variables (x x y x y = xy²). This leads directly to the solution: 4xy².
Further Applications of Algebra Tiles and Algebraic Manipulation
Understanding algebraic manipulation and the use of algebra tiles extends far beyond this single example. These skills are foundational for tackling more complex algebraic expressions, solving equations, and working with polynomials. The ability to visualize algebraic operations using tiles translates to a stronger grasp of abstract mathematical concepts. This foundational knowledge is essential for success in higher-level mathematics and related fields like physics, engineering, and computer science.
Frequently Asked Questions (FAQ)
Q1: Are algebra tiles only useful for simple expressions like 2xy x 2y?
A1: No, algebra tiles are valuable for a wide range of algebraic expressions. They are particularly helpful in visualizing the addition and subtraction of polynomials, factoring, and even solving simple equations. While their usefulness might decrease as complexity drastically increases, they are a strong tool for building an intuitive understanding of algebraic operations.
Q2: Can I use algebra tiles with negative numbers?
A2: Yes, algebra tiles typically include shaded tiles to represent negative numbers. These shaded tiles are used in the same manner as positive tiles, but their interaction follows the rules of arithmetic involving negative numbers. For example, a positive tile and a negative tile of the same type would cancel each other out when added.
Q3: Are there online or digital versions of algebra tiles?
A3: Yes, many interactive online resources and educational software applications provide virtual algebra tiles. These virtual tools offer a similar experience to physical tiles, providing an interactive and flexible learning environment.
Q4: How do algebra tiles help with understanding polynomials?
A4: Algebra tiles provide a visual representation of polynomial terms, making it easier to understand concepts like adding, subtracting, and multiplying polynomials. Visualizing the terms using tiles facilitates understanding the underlying principles of combining like terms and expanding expressions.
Q5: What are some common mistakes to avoid when using algebra tiles?
A5: A common mistake is misinterpreting the dimensions and areas represented by the tiles. Ensure you consistently understand what each tile represents in terms of variables and constants. Another potential error is neglecting the signs of the terms when dealing with negative numbers. Always pay close attention to the positive and negative tiles and their respective rules of interaction.
Conclusion
Mastering algebra is a journey, not a sprint. By utilizing tools like algebra tiles, we can transform abstract mathematical concepts into tangible and understandable representations. The visual approach to solving 2xy x 2y and similar expressions not only strengthens our computational skills but also cultivates a deeper and more intuitive understanding of algebraic principles. This understanding becomes the bedrock for future success in more advanced mathematical studies and applications. Remember the power of visualization, the importance of understanding underlying mathematical principles, and don't hesitate to explore different methods and resources to solidify your grasp of algebra.
Latest Posts
Latest Posts
-
The Am1004 T61 Magnesium Tube
Sep 12, 2025
-
3 4 9 Lab Switching Loop
Sep 12, 2025
-
Diabetes Mellitus System Disorder Template
Sep 12, 2025
-
Which Statement Describes A Ganglion
Sep 12, 2025
-
Abcarian Literature The Human Experience
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2xy X 2y Algebra Tiles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.