14 10 8 18 12
khabri
Sep 10, 2025 · 5 min read
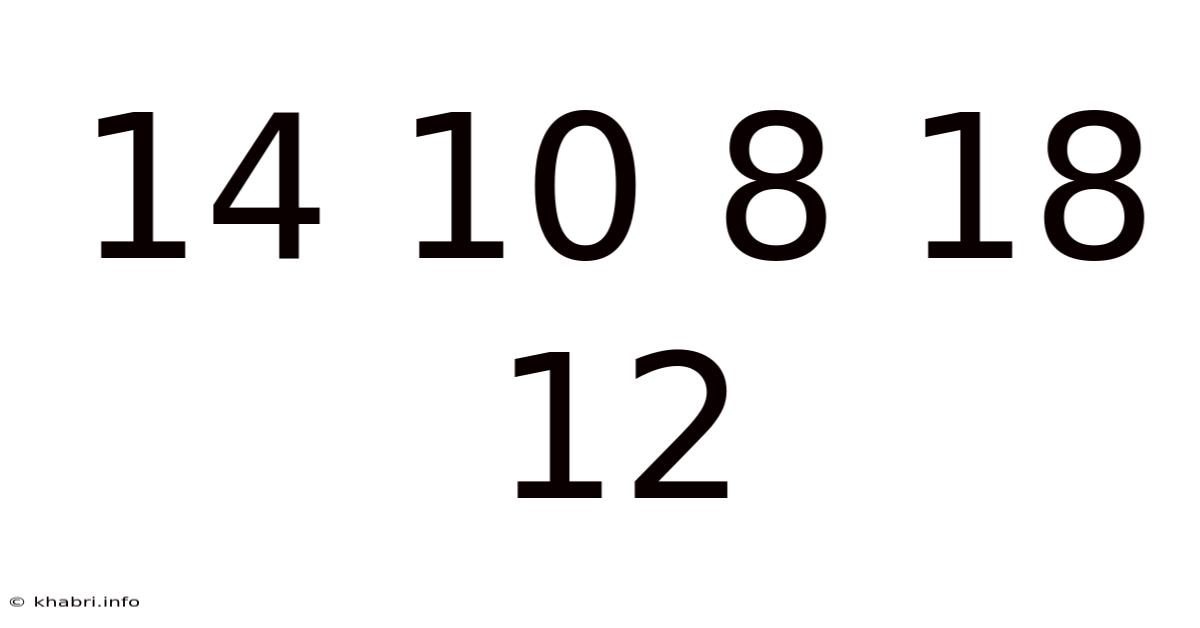
Table of Contents
Unlocking the Mystery: Decoding the Sequence 14 10 8 18 12
The seemingly simple sequence 14, 10, 8, 18, 12 might appear random at first glance. However, beneath the surface lies a fascinating mathematical puzzle that, once solved, reveals the underlying logic and potential for extension. This article will delve deep into this numerical riddle, exploring various approaches to deciphering the pattern, examining potential solutions, and ultimately demonstrating the power of logical reasoning and pattern recognition. We'll uncover not just one, but several possible interpretations, highlighting the beauty of mathematical ambiguity and the importance of considering multiple perspectives.
Introduction: The Allure of Numerical Sequences
Numerical sequences have captivated mathematicians and puzzle enthusiasts for centuries. Their seemingly simple nature often masks intricate relationships and underlying patterns. The beauty of these sequences lies in the challenge they present – the intellectual stimulation of uncovering the hidden rules that govern their progression. The sequence 14, 10, 8, 18, 12 is no exception. It presents a deceptively simple challenge that can lead us down several interesting mathematical paths.
Method 1: Exploring Differences and Patterns
A classic approach to deciphering numerical sequences involves examining the differences between consecutive terms. Let's apply this to our sequence:
- 14 - 10 = 4
- 10 - 8 = 2
- 18 - 8 = 10
- 18 - 12 = 6
The differences (4, 2, 10, 6) don't immediately reveal a clear pattern. However, let's try looking at the second differences – the differences between the differences:
- 4 - 2 = 2
- 10 - 2 = 8
- 10 - 6 = 4
Still, no obvious pattern emerges. This suggests that a simpler, linear relationship might not be the key to unlocking this sequence. We might need to explore more complex mathematical relationships.
Method 2: Investigating Alternate Patterns and Relationships
Perhaps the sequence isn't based on a simple additive or subtractive pattern. Let's consider other possibilities:
-
Prime Factorization: Examining the prime factorization of each number could reveal hidden relationships. However, the prime factorizations of 14 (2 x 7), 10 (2 x 5), 8 (2 x 2 x 2), 18 (2 x 3 x 3), and 12 (2 x 2 x 3) don't immediately suggest a clear pattern.
-
Modular Arithmetic: Exploring remainders after dividing by a specific number might uncover a pattern. Testing different divisors, however, doesn't immediately reveal a consistent relationship.
-
Geometric Relationships: While the sequence doesn't appear to be strictly geometric (each term isn't a constant multiple of the previous term), there might be a more nuanced geometric relationship hidden within.
-
Combinations of Operations: The sequence might be generated by a combination of addition, subtraction, multiplication, and/or division. We could explore various combinations of these operations to see if a pattern emerges. For instance, we might find that the numbers are produced through a series of carefully chosen operations, producing seemingly disparate results.
Method 3: Considering the Possibility of Multiple Underlying Patterns
It's crucial to acknowledge that a single sequence might not have one unique solution. It's entirely possible that different, valid mathematical rules could generate the same sequence. This is a common phenomenon in mathematics, where multiple approaches can lead to the same outcome. Let's consider some potential alternative interpretations:
-
Alternating Patterns: The sequence could be composed of two intertwined sub-sequences. We could separate the sequence into odd and even positions:
- Odd positions: 14, 8, 12... (Potential pattern: alternating addition/subtraction of 6 and 4)
- Even positions: 10, 18... (This sub-sequence is too short to establish a reliable pattern.)
-
Recursive Relationships: A recursive relationship defines each term based on the preceding term(s). For example, a potential (though admittedly complex) recursive relationship might involve a combination of adding and subtracting values based on the previous terms' properties.
-
Hidden Codes or Ciphers: While less likely in a purely mathematical context, the sequence could represent a coded message, where each number corresponds to a letter or symbol using a substitution cipher. This possibility requires additional information or context.
A Deeper Dive: Advanced Mathematical Approaches
For a more rigorous investigation, more advanced mathematical techniques might be employed. These could include:
-
Generating Functions: Generating functions are power series whose coefficients encode the terms of a sequence. Analyzing the generating function could reveal insights into the underlying structure of the sequence.
-
Difference Equations: Difference equations relate consecutive terms of a sequence. Finding a difference equation that fits the given sequence could provide a formal mathematical description of its structure.
-
Transformations: Applying mathematical transformations (like Fourier transforms or Laplace transforms) could reveal hidden periodicities or patterns. However, these approaches require a significant level of mathematical sophistication.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct answer? A: No, there might be multiple ways to generate the sequence. Mathematical ambiguity often allows for multiple valid solutions.
-
Q: What if more numbers were added to the sequence? A: Additional terms would provide more data, potentially clarifying the underlying pattern or ruling out certain hypotheses.
-
Q: Are there any real-world applications for solving such sequences? A: Understanding patterns in numerical sequences is crucial in various fields, including cryptography, signal processing, and predictive modeling.
Conclusion: Embracing the Ambiguity and the Journey
The sequence 14, 10, 8, 18, 12 presents a compelling challenge. While we haven't definitively identified the single, undeniable pattern, the process of investigating this sequence demonstrates the importance of employing multiple approaches, considering different mathematical concepts, and embracing the possibility of multiple solutions. The journey of exploring this seemingly simple sequence has been a valuable exercise in mathematical reasoning, highlighting the creativity and persistence needed to unravel complex puzzles. The true value lies not only in finding a potential solution, but in the process of exploration and the development of problem-solving skills. This exercise demonstrates the beauty and intricacy hidden within even the simplest-appearing numerical sequences, reminding us that the quest for understanding often leads to unexpected and rewarding discoveries. Further exploration and the addition of more numbers to the sequence could potentially reveal even more intricate and fascinating underlying structures.
Latest Posts
Latest Posts
-
Lesson Outline Lesson 2 Answers
Sep 10, 2025
-
Which Statement Describes A Sarcomere
Sep 10, 2025
-
Lab Exercise 41 Respiratory Structures
Sep 10, 2025
-
In Email Marketing Churn Is
Sep 10, 2025
-
Getitem Normally Implemented In Torch
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 14 10 8 18 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.