11 3/4 Divided By 2
khabri
Sep 13, 2025 · 5 min read
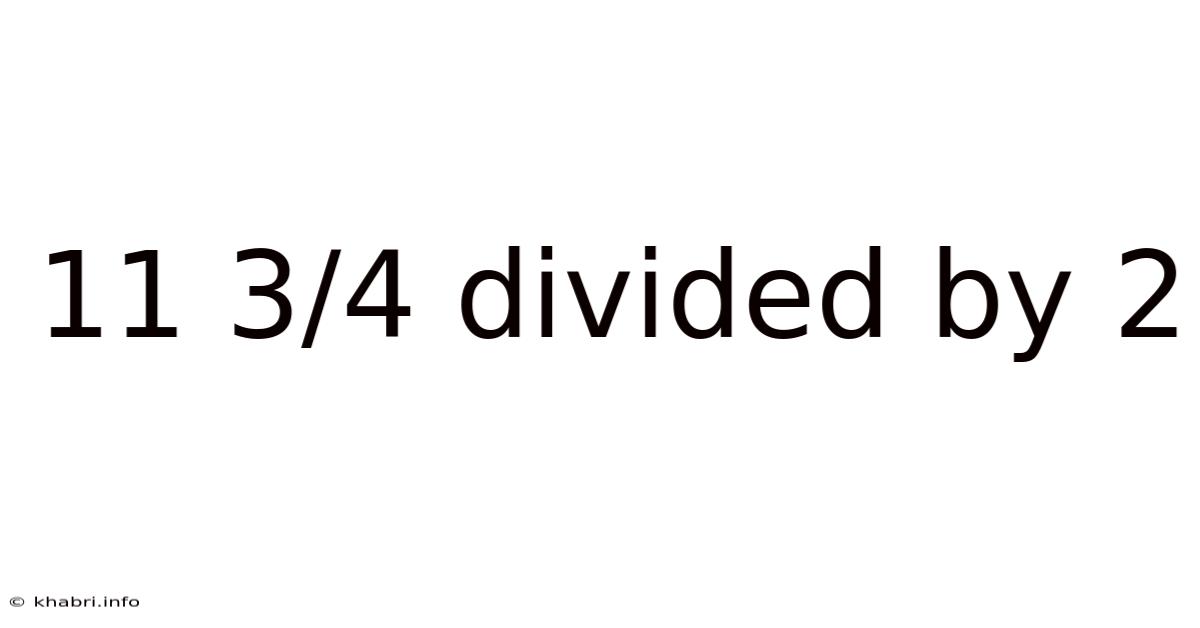
Table of Contents
11 3/4 Divided by 2: A Comprehensive Guide to Fraction Division
Dividing mixed numbers can seem daunting, especially when fractions are involved. But fear not! This comprehensive guide will walk you through the process of solving 11 3/4 divided by 2, explaining each step clearly and providing extra context to build your understanding of fraction division. We'll explore different methods, delve into the underlying mathematical principles, and answer frequently asked questions. By the end, you'll not only know the answer but also possess a solid grasp of this fundamental mathematical concept.
Understanding Mixed Numbers and Fractions
Before we tackle the division, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 11 3/4. This represents 11 whole units plus an additional 3/4 of a unit. A fraction, on the other hand, expresses a part of a whole, with the numerator representing the number of parts and the denominator representing the total number of parts in the whole.
In our problem, 11 3/4, the whole number is 11, the numerator is 3, and the denominator is 4. Understanding this foundation is crucial for successfully dividing mixed numbers.
Method 1: Converting to Improper Fractions
The most straightforward method for dividing mixed numbers is to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Steps:
-
Convert the mixed number to an improper fraction: To do this, multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same.
For 11 3/4: (11 x 4) + 3 = 47. Therefore, 11 3/4 becomes 47/4.
-
Rewrite the division problem: Our problem now becomes 47/4 ÷ 2.
-
Convert the whole number to a fraction: Rewrite 2 as a fraction: 2/1.
-
Invert the divisor and multiply: When dividing fractions, we invert (flip) the second fraction (the divisor) and then multiply. This means we change 2/1 to 1/2 and multiply:
47/4 x 1/2 = (47 x 1) / (4 x 2) = 47/8
-
Simplify (if possible): In this case, 47/8 is an improper fraction. We can convert it back to a mixed number by dividing the numerator by the denominator:
47 ÷ 8 = 5 with a remainder of 7. So, 47/8 is equivalent to 5 7/8.
Therefore, 11 3/4 divided by 2 equals 5 7/8.
Method 2: Dividing the Whole Number and Fraction Separately
This method involves dividing the whole number and fractional parts separately and then combining the results. While seemingly simpler, it requires careful attention to detail.
Steps:
-
Divide the whole number: Divide the whole number part of the mixed number by the divisor: 11 ÷ 2 = 5 with a remainder of 1.
-
Convert the remainder to a fraction: The remainder of 1 becomes the numerator of a fraction with the original denominator of 4: 1/4.
-
Divide the fractional part: Divide the fractional part of the mixed number by the divisor: 3/4 ÷ 2 = 3/4 x 1/2 = 3/8
-
Combine the results: Add the whole number result from step 1 to the fractional result from step 3: 5 + 3/8 = 5 3/8. This result is INCORRECT. The error arises from incorrectly dividing the remainder as a fraction. This method, though conceptually simple, is prone to mistakes and should be approached with extreme caution. Method 1 is far more reliable.
The Mathematical Principles Behind Fraction Division
The core principle behind dividing fractions is the concept of reciprocals (or multiplicative inverses). The reciprocal of a fraction is found by swapping the numerator and denominator. When dividing by a fraction, we multiply by its reciprocal. This is because division is the inverse operation of multiplication.
Consider the problem a/b ÷ c/d. To solve this, we multiply a/b by the reciprocal of c/d, which is d/c:
(a/b) x (d/c) = (a x d) / (b x c)
This principle applies even when one of the numbers is a whole number, as we saw in Method 1, where we converted 2 to 2/1 and then used its reciprocal, 1/2.
Decimal Approach (for Approximation)
While not as precise for fractions, converting to decimals can provide a reasonable approximation.
Steps:
-
Convert the mixed number to a decimal: 11 3/4 = 11.75
-
Divide the decimal: 11.75 ÷ 2 = 5.875
This decimal, 5.875, is equivalent to 5 7/8, confirming our previous results. However, this approach may lead to rounding errors, especially with more complex fractions.
Frequently Asked Questions (FAQ)
-
Can I use a calculator to solve this? Yes, most calculators can handle fraction division. However, understanding the underlying mathematical process is crucial for problem-solving beyond simple calculations.
-
Why is it important to learn fraction division? Fraction division is fundamental to various aspects of mathematics and its applications in real-world scenarios, including cooking, construction, engineering, and data analysis. Mastering this skill strengthens your overall mathematical proficiency.
-
What if the divisor was a fraction instead of a whole number? The process remains the same: convert all mixed numbers to improper fractions, invert the divisor (second fraction), and multiply.
-
Are there other methods to divide mixed numbers? While the methods described above are the most common and efficient, alternative methods exist, often involving long division or visual representations like area models. However, these methods are generally less efficient for mixed numbers.
Conclusion
Dividing 11 3/4 by 2 results in 5 7/8. This seemingly simple problem provides a valuable opportunity to reinforce understanding of fractions, mixed numbers, and the fundamental principles of fraction division. Mastering fraction division is not just about finding the correct answer; it’s about developing a deeper comprehension of mathematical concepts and building a solid foundation for more advanced mathematical explorations. Remember to practice different methods to find the approach that best suits your learning style and always double-check your work! Consistent practice will solidify your understanding and make you a confident fraction divider.
Latest Posts
Latest Posts
-
Is Cacl2 An Ionic Compound
Sep 13, 2025
-
Adjective That Starts With I
Sep 13, 2025
-
Understanding How Electrostatic Forces Cancel
Sep 13, 2025
-
Art Labeling Activity Neuron Structure
Sep 13, 2025
-
Classical Electrodynamics Jackson 3rd Edition
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 11 3/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.