10 X 3 6 2x
khabri
Sep 13, 2025 · 6 min read
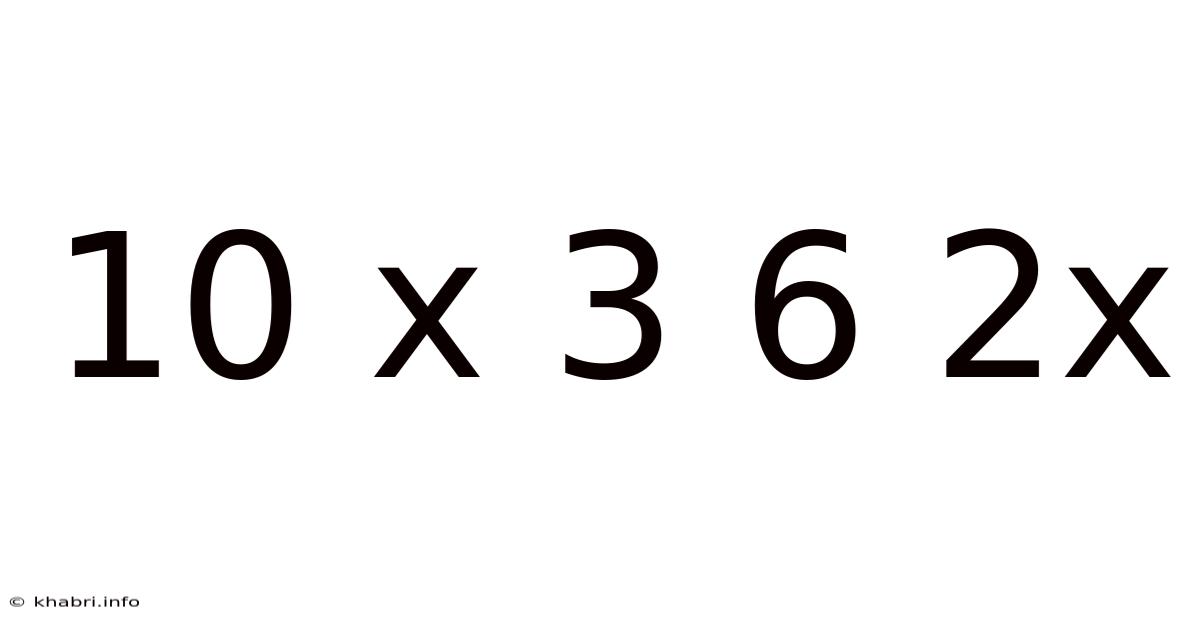
Table of Contents
Decoding the Enigma: A Deep Dive into "10 x 3 6 2x"
The seemingly simple string "10 x 3 6 2x" might appear innocuous at first glance. However, depending on the context, it could represent a variety of mathematical expressions, codes, or even a cryptic message. This article aims to explore the multiple interpretations of this sequence, providing a comprehensive analysis of its potential meanings and demonstrating how context is crucial in deciphering such ambiguous expressions. We will delve into the realms of arithmetic, algebra, combinatorics, and even cryptography to unlock the secrets hidden within these six simple characters.
Understanding the Potential Interpretations
The lack of clear operational symbols and the presence of 'x' as both a variable and a multiplication symbol creates significant ambiguity. Let's break down the possible interpretations:
1. As a Simple Arithmetic Expression:
The most straightforward interpretation is to consider 'x' as representing multiplication. However, the arrangement requires careful consideration of operator precedence. We could have several possibilities:
-
Interpretation A: (10 x 3) + 6 + 2: This interpretation follows the standard order of operations (PEMDAS/BODMAS), performing multiplication before addition. The result would be 30 + 6 + 2 = 38.
-
Interpretation B: 10 x (3 + 6 + 2): This interpretation prioritizes the addition within parentheses first. The calculation would be 10 x 11 = 110.
-
Interpretation C: 10 x 3 x 6 x 2: This assumes implicit multiplication between all numbers. The result is a much larger number: 360.
-
Interpretation D: Other combinations: Numerous other combinations of addition and multiplication are possible depending on how the 'x' is interpreted and where implied multiplication might be assumed.
2. As an Algebraic Equation:
If we interpret 'x' as a variable, the expression becomes significantly more complex. We'd need additional information or constraints to solve for 'x'. For example:
-
Equation A: 10x + 3 = 6 + 2x: This is a linear equation. To solve it, we would rearrange the terms: 8x = 3, therefore x = 3/8 or 0.375.
-
Equation B: 10x³ + 6 = 2x: This is a cubic equation, requiring more advanced algebraic techniques to solve. There could be multiple solutions for 'x' in this case.
-
Equation C: Other possibilities: Various other algebraic equations could be formulated depending on where we place the equal sign and how we interpret the numbers and the 'x' variable.
3. As a Code or Cipher:
"10 x 3 6 2x" could also be part of a code or cipher. Without a key or more context, deciphering it would be highly speculative. Possible approaches could involve:
-
Substitution Cipher: Each number might represent a letter of the alphabet (e.g., A=1, B=2, etc.), or a combination of letters.
-
Caesar Cipher: Each number could be shifted by a certain amount to reveal a hidden message.
-
More Complex Ciphers: The sequence might be part of a more sophisticated cipher requiring a decryption algorithm.
4. As a Combinatorial Problem:
In combinatorics, the sequence could represent various arrangements or selections. For example:
-
Permutations: The numbers could represent elements to be arranged in a specific order, although the presence of 'x' complicates this significantly.
-
Combinations: The sequence could indicate a selection from a larger set. Again, the 'x' adds complexity, potentially representing a wildcard or an unknown quantity.
A Detailed Examination of Algebraic Interpretations
Let's delve deeper into the algebraic possibilities, focusing on solving for 'x'. As we've seen, the interpretation of the expression is crucial. The presence of 'x' as both a variable and a multiplication symbol introduces a high degree of ambiguity, requiring careful consideration of the underlying equation's structure.
Solving Linear Equations:
Consider the equation 10x + 3 = 6 + 2x. Solving for 'x' involves isolating the variable on one side of the equation:
-
Subtract 2x from both sides: 8x + 3 = 6
-
Subtract 3 from both sides: 8x = 3
-
Divide both sides by 8: x = 3/8 = 0.375
Solving Cubic Equations:
The equation 10x³ + 6 = 2x presents a more challenging scenario. This is a cubic equation, meaning it has a degree of 3. Solving cubic equations often requires more advanced techniques, such as the cubic formula or numerical methods. Rearranging the equation, we get:
10x³ - 2x + 6 = 0
Solving this cubic equation analytically can be quite complex. Numerical methods, such as the Newton-Raphson method, are often used to approximate the roots of such equations. These methods involve iterative calculations to progressively refine an estimate of the solution.
The Importance of Context
The true meaning of "10 x 3 6 2x" is entirely dependent on the context in which it appears. Without further information, it remains an ambiguous expression with multiple valid interpretations. The key to deciphering its meaning lies in understanding the source and the intended purpose of the sequence.
For example, if found in a math textbook, it likely represents a problem requiring the application of algebraic or arithmetic principles. If encountered in a coding context, it might be a fragment of code or an encrypted message. If part of a puzzle or riddle, the context of the surrounding clues will be crucial in interpreting its meaning.
Frequently Asked Questions (FAQ)
Q: Can "x" represent both multiplication and a variable simultaneously?
A: Mathematically, this is ambiguous and generally avoided in formal notation. The use of "x" in this manner requires very clear context to avoid confusion. In most cases, it would be considered poor mathematical practice.
Q: Are there any other possible interpretations besides arithmetic and algebra?
A: Yes, as discussed earlier, it could represent a code, a cipher, a combinatorial problem, or even part of a larger symbolic system. The possibilities are quite extensive depending on context.
Q: How can I solve the cubic equation 10x³ - 2x + 6 = 0?
A: Solving cubic equations analytically is complex. It usually involves the cubic formula or numerical methods like the Newton-Raphson method which require iterative calculations to approximate solutions. Software or calculators with algebraic capabilities can assist in finding these solutions.
Conclusion
The seemingly simple string "10 x 3 6 2x" reveals a fascinating depth of ambiguity. Its interpretation hinges entirely on context. We've explored various possibilities, from straightforward arithmetic operations to complex algebraic equations and even cryptic codes. This exercise highlights the importance of clear communication and unambiguous notation, particularly in mathematical and computational contexts. Without clarifying the intended meaning and providing sufficient contextual information, the true value of "10 x 3 6 2x" remains elusive. The key takeaway is that seemingly simple sequences can hold immense complexity, and understanding the context is vital for proper interpretation. Further investigation and more details would be needed to definitively unlock the secrets hidden within this intriguing sequence of numbers and symbols.
Latest Posts
Latest Posts
-
External Users Of Accounting Information
Sep 13, 2025
-
Mr Prentice Has Many Clients
Sep 13, 2025
-
6 Steps For Hypothesis Testing
Sep 13, 2025
-
Mla Citation For A Song
Sep 13, 2025
-
Fundamentals Of Management 10th Edition
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 10 X 3 6 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.